
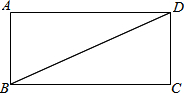
 (1)在图中作出△CDB沿对角线BD所在的直线对折后的△C1DB,C点的对应点为C1(用尺规作图,保留清晰的作图痕迹,不写作法);
(1)在图中作出△CDB沿对角线BD所在的直线对折后的△C1DB,C点的对应点为C1(用尺规作图,保留清晰的作图痕迹,不写作法);分析 (1)利用基本作图(过一点作直线的垂线)作CH⊥BD于H,延长CH到C1点,使C1H=CH,连结BC1、DC1,则△C1DB与△CBD关于直线BD对称;
(2)先利用三角函数的定义计算出∠ABE=30°,则∠CBE=60°,再根据折叠的性质得到∠CBD=∠C1BD,所以∠DBC=$\frac{1}{2}$∠CBE=30°.
解答 解:(1)如图,△C1DB为所作;
(2)在Rt△ABE中,∵sin∠ABE=$\frac{AE}{BE}$=$\frac{AE}{2AE}$=$\frac{1}{2}$,
∴∠ABE=30°,
∴∠CBE=60°,
∵△CDB沿对角线BD所在的直线对折后得到△C1DB,
∴∠CBD=∠C1BD,
∴∠DBC=$\frac{1}{2}$∠CBE=30°.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了折叠的性质.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:选择题
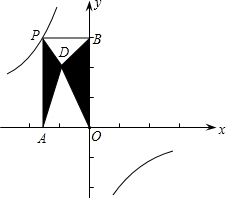 如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )
如图,P是反比例函数y=$\frac{k}{x}$的图象上任意点,过点P分别作坐标轴的垂线与坐标轴构成矩形OAPB,点D是对角线OP上的动点,连接DA、DB,若图中阴影部分的面积是5,则反比例函数的关系式是( )| A. | y=-$\frac{5}{x}$ | B. | y=-$\frac{8}{x}$ | C. | y=-$\frac{10}{x}$ | D. | y=-$\frac{12}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
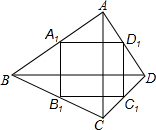 如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.
如图,四边形ABCD的两条对角线AC,BD互相垂直,A1,B1,C1,D1是四边形ABCD对应边上的中点.如果AC=8,BD=10,那么四边形A1B1C1D1周长为18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:
2006年某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部回收.将消费者年收入情况整理后,绘制成如图所示的表格:| 年收入(万元) | 1.2 | 1.8 | 3 | 5 | 10 |
| 被调查的消费者人数(人) | 200 | 500 | 200 | 70 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
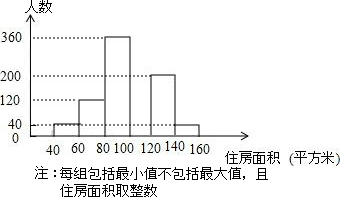
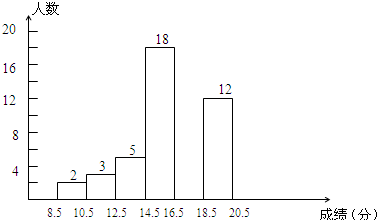 某初中九年级共有700名学生,进行体育测试,包括两项内容:立定跳远和长跑(男子1000米、女子800米),满分各为10分,共20分,得分取整数.随机抽取50名学生的测试成绩进行统计分析,将所有成绩由低到高分成6组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
某初中九年级共有700名学生,进行体育测试,包括两项内容:立定跳远和长跑(男子1000米、女子800米),满分各为10分,共20分,得分取整数.随机抽取50名学生的测试成绩进行统计分析,将所有成绩由低到高分成6组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com