
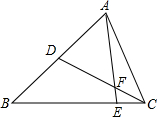
 如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为30.
如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为30. 分析 作DG∥AE,交BC于G,得出△CEF∽△CGD,根据题意求得S△CGD=9,进而结合同高不等底的三角形面积关系求出S△BDG=6,即可求得S△BCD=15,得到△ABC的面积为30.
解答 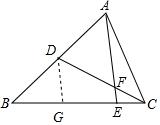 解:作DG∥AE,交BC于G,
解:作DG∥AE,交BC于G,
∵AD=BD,
∴BG=EG,
∵BE=4EC,
∴GE=2EC,
∴$\frac{EC}{GC}$=$\frac{1}{3}$,
∵DG∥AE,
∴△CEF∽△CGD,
∴$\frac{{S}_{△CEF}}{{S}_{△CGD}}$=$\frac{1}{9}$,
∵△CEF的面积为1,
∴S△CGD=9,
∵BG:CG=2:3,
∴S△BDG=6,
∴S△BCD=9+6=15,
∴S△ABC=2S△BCD=30.
故答案为:30.
点评 本题考查了三角形相似的判定和性质,同高不等底的三角形面积关系,作出辅助性构建相似三角形是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
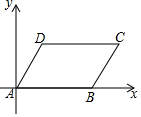 如图,在直角坐标系中,?ABCD的四个顶点的坐标分别为A(0,0),B(6,0),C (8,4),D(2,4).若直线y=3x+b把?ABCD的面积平分成相等的两部分,则b的值是-10.
如图,在直角坐标系中,?ABCD的四个顶点的坐标分别为A(0,0),B(6,0),C (8,4),D(2,4).若直线y=3x+b把?ABCD的面积平分成相等的两部分,则b的值是-10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
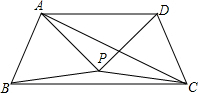 如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).
如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
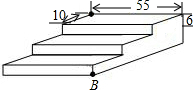 如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.
如图是一个三级台阶,它的每一级的长、宽、高分别等于55dm、10dm和6dm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁从A点出发沿着台阶爬到B点的最短距离是73dm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
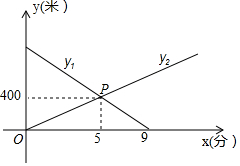 甲从A地出发匀速走向B地,同时乙从B地出发按同一路线匀速走向A地,如图所示,y1、y2分别表示甲、乙离B地的距离(米)与行走时间x(分)之间的关系.
甲从A地出发匀速走向B地,同时乙从B地出发按同一路线匀速走向A地,如图所示,y1、y2分别表示甲、乙离B地的距离(米)与行走时间x(分)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
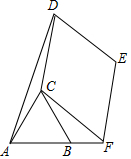 如图,点B在线段AF上,等边三角形ABC边长为1,菱形CDEF边长为$\sqrt{7}$,且∠DCF=120°.则△ACD的面积是$\frac{\sqrt{3}}{2}$.
如图,点B在线段AF上,等边三角形ABC边长为1,菱形CDEF边长为$\sqrt{7}$,且∠DCF=120°.则△ACD的面积是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
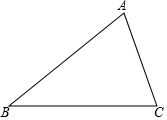 尺规作图:如图,已知△ABC,求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,保留作图痕迹)
尺规作图:如图,已知△ABC,求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com