
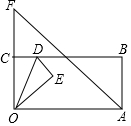
 如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10. 分析 如图,作EM⊥OF于M.设EM=x.首先证明EM=FM,在Rt△OEM中,理由勾股定理求出x即可解决问题.
解答 解:如图,作EM⊥OF于M.设EM=x.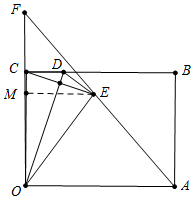
∵四边形OABC是矩形,
∴∠AOC=90°,
∵OA=OF=7,
∴∠F=∠FAO=45°,
∵∠FME=∠FOA=90°,
∴∠FEM=45°=∠F,
∴ME=MF=x,OM=7-x,
在Rt△OEM中,∵OM2+EM2=OE2,
∴x2+(7-x)2=52,
解得x=3或4,
∴S△COE=$\frac{1}{2}$×5×3=$\frac{15}{2}$或∴S△COE=$\frac{1}{2}$×5×4=10,
故答案为$\frac{15}{2}$或10
点评 本题考查翻折变换、矩形的性质、等腰直角三角形的性质、勾股定理、三角形的面积等知识,解题的关键是学会添加常用辅助线,构建方程解决问题,属于中考填空题中的压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①、②是真命题 | B. | ②、③是真命题 | C. | ①、③是假命题 | D. | 以上结论都错 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.
如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=6}\\{x=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+z=0}\\{3x-y=\frac{1}{5}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{1}{x}+y=5}\\{2x-5y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3}\\{xy=1}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com