
����Ŀ��ij��ۼӹ����ӹ�����ۣ���ÿ����װ10g��۵Ĵ���װ��200���������أ���������������10kg����������ʾ���������ڱ�����10kg���ø�����ʾ�������¼����
���������ƫ��(kg) | ��1.5 | ��1 | ��0.5 | 0 | 0.5 | 1 | 2 |
����(��) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)��������۵���������
(2)���100kgС��ӹ�80kg��ۣ���ô����������ɶ���ǧ��С��ӹ��ģ�
 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������
��1�����Ķ����֡���ͼ�٣���������ABCD����࣬�������ȱ�������ABE��ADF������ED��FC���ڵ�M����ͼ�С�ADE�ա�DFC����֪ED=FC����á�DMC= ��
��2������չӦ�á���ͼ�ڣ��ھ���ABCD��AB��BC������࣬�������ȱ�������ABE��ADF������ED��FC���ڵ�M�� 
��i����֤��ED=FC��
��ii������ADE=20�㣬���DMC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC�У���CAB=90�㣬AB=AC��
��1����ͼ1��P��Q��BC�������㣬AP=AQ����BAP=20��������AQB�Ķ�����
��2����P��Q��BC���������㣨����B��C�غϣ�����P�ڵ�Q��࣬��AP=AQ����Q����ֱ��AC�ĶԳƵ�ΪM������AM��PM��
�������⽫ͼ2��ȫ��
��С��ͨ���۲��ʵ�飬������룺�ڵ�P��Q�˶��Ĺ����У�ʼ����PM=![]() PA���������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ�����֤�������˼·��
PA���������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ�����֤�������˼·��
������Ҫ��֤��PM=![]() PA��ֻ��֤��APMΪ����ֱ�������Σ�
PA��ֻ��֤��APMΪ����ֱ�������Σ�
������Ҫ��֤����APMΪ����ֱ�������Σ�ֻ��֤��PAM=90�㣬PA=AM��
��
��ο������˼·������С��֤��PM=![]() PA��
PA��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̨��Ϊ�ӿ���ũ�彨�������������������A��B�����ׯ������ȫ��Ľ�������Ԥ��������һ��A��������ׯ��һ��B��������ׯ�����ʽ�300��Ԫ�����������2��A���ׯ��5��B���ׯ��Ͷ���ʽ�1140��Ԫ��
��1������һ��A��������ׯ��һ��B��������ׯ������ʽ�ֱ��Ƕ�����Ԫ��
��2�����ճ���Ľ�3��A��������ׯ��6��B��������ׯ�����ʽ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����B��6��0����ֱ��AB��ֱ��OA�ཻ�ڵ�A��4��2��������M��·��O��A��C�˶���
��1����ֱ��AB�Ľ���ʽ��
��2������OAC�������
��3������OMC���������OAC�������![]() ʱ�������ʱ��M�����꣮
ʱ�������ʱ��M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
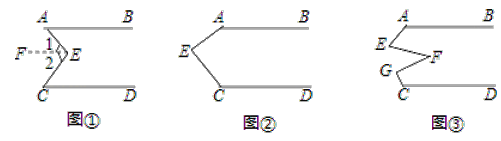
����Ŀ������֪����ͼ����AB��CD����E��ֱ��AB��CD֮�䣬����AE��BE����˵����BEE+��DCE����AEC����������������Ľ�����̣����������Ľ�����̣�����գ����ɻ���ѧʽ����
�⣺��ͼ�٣�����E��EF��AB
���BAE����1���� ����
��AB��CD���� ����
��CD��EF���� ����
���2����DCE
���BAE+��DCE����1+��2���� ����
���BAE+��DCE����AEC
��̽��������E����ͼ�ڵ�λ��ʱ�������������䣬��˵����AEC+��FGC+��DCE��360�㣻
��Ӧ�ã���E��F��G��ֱ��AB��CD֮�䣬����AE��EF��FG��CG�������������䣬��ͼ�ۣ�����EFG��36�������BAE+��AEF+��FGC+��DCG���� ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ۼӹ����ӹ�����ۣ���ÿ����װ10g��۵Ĵ���װ��200���������أ���������������10kg����������ʾ���������ڱ�����10kg���ø�����ʾ�������¼����
���������ƫ��(kg) | ��1.5 | ��1 | ��0.5 | 0 | 0.5 | 1 | 2 |
����(��) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)��������۵���������
(2)���100kgС��ӹ�80kg��ۣ���ô����������ɶ���ǧ��С��ӹ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC=90������PΪ����BC������һ�㣨��P���B���غϣ����ֱ���AB��APΪ���ڡ�ABC���ڲ����ȱߡ�ABE�͡�APQ������QE���ӳ���BP�ڵ�F��
��1����ͼ1����AB=![]() ����A��E��Pǡ����һ��ֱ����ʱ����EF�ij���ֱ��д���������
����A��E��Pǡ����һ��ֱ����ʱ����EF�ij���ֱ��д���������
��2����ͼ2������PΪ����BC������һ��ʱ����֤��BF=EF��
��3����AB=![]() ����BP=2����QF�ij���
����BP=2����QF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊa�������Σ���G��E�ֱ��DZ�AB��BC���е㣬��AEF=90�㣬��EF����������ǵ�ƽ����CF�ڵ�F�� 
��1��֤������AGE�ա�ECF��
��2�����AEF�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com