
甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打
第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),
并根据该实验写出一个发生概率与(1)所求概率相同的事件.
解:(1)从中选出两位同学打第一场比赛所有可能出现的结果有:
|
第一位 | 甲 | 乙 | 丙 | 丁 |
| 甲 | —— | (甲,乙) | (甲,丙) | (甲,丁) |
| 乙 | (乙,甲) | —— | (乙,丙) | (乙,丁) |
| 丙 | (丙,甲) | (丙,乙) | —— | (丙,丁) |
| 丁 | (丁,甲) | (丁,乙) | (丁,丙) | —— |
共有12种,它们出现的可能性相同.所有的结果中,满足“恰好选中甲、乙两位同学”(记为事件A)的结果有2种,所以P(A)=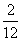 =
= .
.
(2)本题答案不唯一,下列解法供参考.
法一:在不透明的袋中,放入2个红色1个白色3个乒乓球,它们除颜色外都一样,
摇匀.第一次摸出1个球,不放回;第二次摸出1个球记下颜色,放回;第3次摸
出1个球.则三次摸出的球都是红色球的概率.
法二:在不透明的袋子中,放入四个除颜色外完全一样的乒乓球,它们的颜色分别
为红、黄、蓝、黑,摇匀.第一次摸出一个球后,不放回;再从袋中摸出一个球.则两次摸出的球是一红一黄的概率.
法三:在不透明的袋子中,放入2个红色2个白色共4个乒乓球.它们除颜色外都
一样,摇匀.连续摸2次不放回,则两次摸到的球都是红色球的概率.
法四:在不透明的袋子中,放入编号为1、2、3、4、5、6的6个乒乓球,它们除
编号外其它都一样,摇匀.第一次摸出1个球记下颜色后放回;第二次摸出1个球.
则两次摸出颜色相同的球的概率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC
按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
 ②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
 | |||||||
| |||||||
| | |||||||
| |||||||
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于 的一元二次方程
的一元二次方程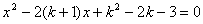 有两个不相等的实数
有两个不相等的实数 根.
根.
(1)求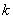 的取值范围;
的取值范围;
(2)当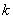 取最小的整数时,求抛物线
取最小的整数时,求抛物线 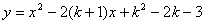 的顶点坐标以及它与
的顶点坐标以及它与 轴的交点坐标;
轴的交点坐标;
(3)将(2)中求得的抛物线在 轴下方的部分沿
轴下方的部分沿 轴翻折到
轴翻折到 轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线
轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线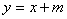 有三个不同公共点时
有三个不同公共点时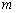 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com