【答案】
分析:(1)根据已知条件选择交点式设出二次函数的解析式.再进一步把它变形为顶点式,则它的顶点坐标满足直线解析式得到关于k、a的方程.根据将这条抛物线先向上平移m个单位,再向右平移m个单位,在顶点式的基础上,左加右减,上加下减的方法得到新的抛物线解析式,再进一步把它的顶点坐标代入直线解析式得到关于k、m的方程.即可求得k、a的值,进一步求得抛物线的解析式;
(2)根据点B'的坐标和点A'的坐标,运用割补法表示出三角形的面积,列方程求解.
解答:解:(1)已知原抛物线经过原点O(0,0)与A(4,0)点,
因此可设原抛物线的表达式为y=ax(x-4).(1分)
配方得y=a(x-2)
2-4a,则其顶点B的坐标为(2,-4a).(2分)
因为顶点B在直线y=kx+2k(k≠0)上,将(2,-4a)代入可得k=-a.(3分)
由题意可知平移后得到的抛物线的顶点B'的坐标为(2+m,-4a+m),即(2+m,4k+m).
因为B'点仍然在直线y=kx+2k上,则4k+m=k(2+m)+2k,
整理得m=km,因为m>0,
所以k=1,(4分)
则a=-1,所以原抛物线的表达式为y=-x(x-4).(或y=-x
2+4x)(5分)
(2)方法一:由(1)知,点B'的坐标为(2+m,4+m),
由题意,点A'的坐标为(4+m,m),(6分)
作B'C垂直于y轴于C,作A'D垂直于y轴于D,(7分)
因为m>0,所以△A'OB'的面积
=△B'OC的面积+梯形B'CDA'的面积-△A'OD的面积
=

(2+m)(4+m)+

(4+m+m)(4+m-2-m)-

m(4+m)
=3m+8,(8分)
由3m+8=6032,
解得m=2008.(10分)
方法二:由(1)知,点B'的坐标为(2+m,4+m),
由题意,点A'的坐标为(4+m,m),(6分)
设直线A'B'的表达式为y=k'x+b,则

解得
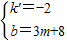
(7分)
则直线A'B'的表达式为y=-2x+3m+8.
设直线A'B'与x轴的交点为C,则点C的坐标为

.(8分)
因为m>0,
所以

>0,y
A'=m>0,y
B'=4+m>0,
所以S
△A'OB'=

OC•yB'-

OC•yA'=

OC(yB'-yA')=

•

•(4+m-m)=3m+8=6032,
解得m=2008.(10分)
点评:注意:抛物线平移的时候,解析式的变形必须在顶点式的基础上进行平移:左加右减,上加下减.即把抛物线y=a(x-h)
2+k向右平移m个单位长度,再向上平移m个单位长度得到的抛物线的解析式是y=a(x-h-m)
2-4a+m;一个点平移的时候,横坐标是左减右加,纵坐标是上加下减.能够运用割补法把在平面直角坐标系中摆放不规则的图形的面积进行求解.

 (2+m)(4+m)+
(2+m)(4+m)+ (4+m+m)(4+m-2-m)-
(4+m+m)(4+m-2-m)- m(4+m)
m(4+m)
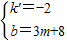 (7分)
(7分) .(8分)
.(8分) >0,yA'=m>0,yB'=4+m>0,
>0,yA'=m>0,yB'=4+m>0, OC•yB'-
OC•yB'- OC•yA'=
OC•yA'= OC(yB'-yA')=
OC(yB'-yA')= •
• •(4+m-m)=3m+8=6032,
•(4+m-m)=3m+8=6032,

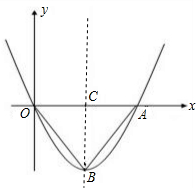 如图,一条抛物线经过原点,且顶点B的坐标(1,-1).
如图,一条抛物线经过原点,且顶点B的坐标(1,-1).