
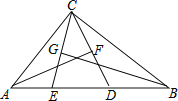
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
【答案】见解析
【解析】试题分析:
(1)由AF垂直平分CD可得AC=AD,再由等腰三角形的“三线合一”可得∠FAB=![]() ∠CAB,同理可得∠GBA=
∠CAB,同理可得∠GBA=![]() ∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-
∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(2)思路同(1)只需把∠ACB=90°换成∠ACB= ![]() 可解得∠DCE=90°-
可解得∠DCE=90°- ![]() .
.

试题解析:
(1)如图,设AF、BG相交于点O,连接CO,
∵AF垂直平分CD,
∴AC=AD,∠CFO=90°,∴∠FAB=![]() ∠CAB.
∠CAB.
同理可得:∠CGO=90°,∠GBA=![]() ∠CBA.
∠CBA.
∴∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=90°+
(180°-∠ACB)=90°+![]() ∠ACB=135°,
∠ACB=135°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-135°
=45°.
(2)同(1)可得∠GOF=90°+![]() ∠ACB=90°+
∠ACB=90°+ ![]() ,∠CFO=90°,∠CGO=90°,
,∠CFO=90°,∠CGO=90°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-(90°+ ![]() )
)
=90°- ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 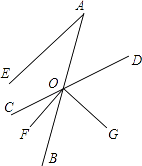
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P(2,2),点A在x轴正半轴上运动,点B在y轴上运动,且PA=PB.
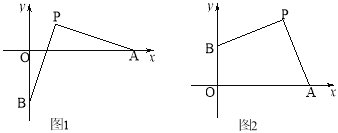
(1)求证:PA⊥PB;
(2)若点A(8,0),求点B的坐标;
(3)求OA – OB的值;
(4)如图2,若点B在y轴正半轴上运动时,直接写出OA+OB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题: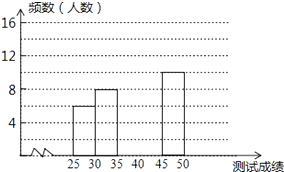
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影《流浪地球》深受人们喜欢,截止到2019年2月17日,票房达到3650000000,则数据3650000000科学记数法表示为( )
A. 0.365×1010B. 36.5×108C. 3.65×108D. 3.65×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com