
| 4 |
| 5 |
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| P1Q1 |
| Q1H |
| HE |
| EN |
| Q2T |
| Q2H |
| EH |
| EN |
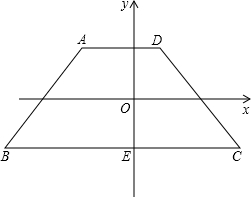
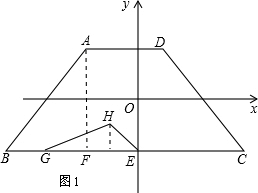 ½ā£ŗ£Ø1£©ČēĶ¼1£¬¹żA×÷AF”ĶBC£®
½ā£ŗ£Ø1£©ČēĶ¼1£¬¹żA×÷AF”ĶBC£®| 4 |
| 5 |
|
|
| 4 |
| 3 |
| 14 |
| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
 µ±t”ä=
µ±t”ä=| 7 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 5 |
| 2 |
| 3 |
| 5 |
| P1Q1 |
| Q1H |
| HE |
| EN |
| 7 |
| 3 |
| 7 |
| 3 |
| Q2T |
| Q2H |
| EH |
| EN |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 2 |
| 3 |


 ½Ģ²ÄČ«½ā×Ö“Ź¾äĘŖĻµĮŠ“š°ø
½Ģ²ÄČ«½ā×Ö“Ź¾äĘŖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 4 | 5 |

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 £®
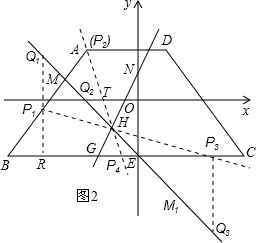
£® ĆėŹ±£¬µćGĶ£Ö¹ŌĖ¶Æ£¬“ĖŹ±Ö±ĻßGHÓėyÖį½»ÓŚµćN£®ĮķŅ»¶ÆµćPæŖŹ¼“ÓB³ö·¢£¬ŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅĢŻŠĪµÄø÷±ßŌĖ¶ÆŅ»ÖÜ£¬¼“ÓÉBµ½A£¬Č»ŗóÓÉAµ½D£¬ŌŁÓÉDµ½C£¬×īŗóÓÉC»Ųµ½B£ØµćPæÉŅŌÓėĢŻŠĪµÄø÷¶„µćÖŲŗĻ£©£®Éč¶ÆµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬µćMĪŖÖ±ĻßHEÉĻČĪŅāŅ»µć£ØµćM²»ÓėµćHÖŲŗĻ£©£¬ŌŚµćPµÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĖłÓŠÄÜŹ¹”ĻPHMÓė”ĻHNEĻąµČµÄtµÄÖµ£®
ĆėŹ±£¬µćGĶ£Ö¹ŌĖ¶Æ£¬“ĖŹ±Ö±ĻßGHÓėyÖį½»ÓŚµćN£®ĮķŅ»¶ÆµćPæŖŹ¼“ÓB³ö·¢£¬ŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅĢŻŠĪµÄø÷±ßŌĖ¶ÆŅ»ÖÜ£¬¼“ÓÉBµ½A£¬Č»ŗóÓÉAµ½D£¬ŌŁÓÉDµ½C£¬×īŗóÓÉC»Ųµ½B£ØµćPæÉŅŌÓėĢŻŠĪµÄø÷¶„µćÖŲŗĻ£©£®Éč¶ÆµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬µćMĪŖÖ±ĻßHEÉĻČĪŅāŅ»µć£ØµćM²»ÓėµćHÖŲŗĻ£©£¬ŌŚµćPµÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĖłÓŠÄÜŹ¹”ĻPHMÓė”ĻHNEĻąµČµÄtµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2011Äźŗž±±Ź”¶õÖŻŹŠŹÆÉ½ÖŠŃ§ÖŠæ¼ŹżŃ§Ä£ÄāŹŌ¾ķ£ØĪ壩£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
 £®
£® ĆėŹ±£¬µćGĶ£Ö¹ŌĖ¶Æ£¬“ĖŹ±Ö±ĻßGHÓėyÖį½»ÓŚµćN£®ĮķŅ»¶ÆµćPæŖŹ¼“ÓB³ö·¢£¬ŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅĢŻŠĪµÄø÷±ßŌĖ¶ÆŅ»ÖÜ£¬¼“ÓÉBµ½A£¬Č»ŗóÓÉAµ½D£¬ŌŁÓÉDµ½C£¬×īŗóÓÉC»Ųµ½B£ØµćPæÉŅŌÓėĢŻŠĪµÄø÷¶„µćÖŲŗĻ£©£®Éč¶ÆµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬µćMĪŖÖ±ĻßHEÉĻČĪŅāŅ»µć£ØµćM²»ÓėµćHÖŲŗĻ£©£¬ŌŚµćPµÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĖłÓŠÄÜŹ¹”ĻPHMÓė”ĻHNEĻąµČµÄtµÄÖµ£®
ĆėŹ±£¬µćGĶ£Ö¹ŌĖ¶Æ£¬“ĖŹ±Ö±ĻßGHÓėyÖį½»ÓŚµćN£®ĮķŅ»¶ÆµćPæŖŹ¼“ÓB³ö·¢£¬ŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅĢŻŠĪµÄø÷±ßŌĖ¶ÆŅ»ÖÜ£¬¼“ÓÉBµ½A£¬Č»ŗóÓÉAµ½D£¬ŌŁÓÉDµ½C£¬×īŗóÓÉC»Ųµ½B£ØµćPæÉŅŌÓėĢŻŠĪµÄø÷¶„µćÖŲŗĻ£©£®Éč¶ÆµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬µćMĪŖÖ±ĻßHEÉĻČĪŅāŅ»µć£ØµćM²»ÓėµćHÖŲŗĻ£©£¬ŌŚµćPµÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĖłÓŠÄÜŹ¹”ĻPHMÓė”ĻHNEĻąµČµÄtµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2007ÄźŗŚĮś½Ź”¹ž¶ū±õŹŠÖŠæ¼ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
 £®
£® ĆėŹ±£¬µćGĶ£Ö¹ŌĖ¶Æ£¬“ĖŹ±Ö±ĻßGHÓėyÖį½»ÓŚµćN£®ĮķŅ»¶ÆµćPæŖŹ¼“ÓB³ö·¢£¬ŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅĢŻŠĪµÄø÷±ßŌĖ¶ÆŅ»ÖÜ£¬¼“ÓÉBµ½A£¬Č»ŗóÓÉAµ½D£¬ŌŁÓÉDµ½C£¬×īŗóÓÉC»Ųµ½B£ØµćPæÉŅŌÓėĢŻŠĪµÄø÷¶„µćÖŲŗĻ£©£®Éč¶ÆµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬µćMĪŖÖ±ĻßHEÉĻČĪŅāŅ»µć£ØµćM²»ÓėµćHÖŲŗĻ£©£¬ŌŚµćPµÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĖłÓŠÄÜŹ¹”ĻPHMÓė”ĻHNEĻąµČµÄtµÄÖµ£®
ĆėŹ±£¬µćGĶ£Ö¹ŌĖ¶Æ£¬“ĖŹ±Ö±ĻßGHÓėyÖį½»ÓŚµćN£®ĮķŅ»¶ÆµćPæŖŹ¼“ÓB³ö·¢£¬ŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŃŲ×ÅĢŻŠĪµÄø÷±ßŌĖ¶ÆŅ»ÖÜ£¬¼“ÓÉBµ½A£¬Č»ŗóÓÉAµ½D£¬ŌŁÓÉDµ½C£¬×īŗóÓÉC»Ųµ½B£ØµćPæÉŅŌÓėĢŻŠĪµÄø÷¶„µćÖŲŗĻ£©£®Éč¶ÆµćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬µćMĪŖÖ±ĻßHEÉĻČĪŅāŅ»µć£ØµćM²»ÓėµćHÖŲŗĻ£©£¬ŌŚµćPµÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Ēó³öĖłÓŠÄÜŹ¹”ĻPHMÓė”ĻHNEĻąµČµÄtµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com