
【题目】如图,圆E是三角形ABC的外接圆, ∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程).

【答案】(1)![]() ;(2)抛物线的解析式为y=-x2+x+6.(3)满足条件的点P有6个.
;(2)抛物线的解析式为y=-x2+x+6.(3)满足条件的点P有6个.
【解析】试题分析:(1)如图1中,连接EB、EC.由BC=OB+OC=5,∠BEC=2∠BC=90°,可知EB的长,进而得到结论.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.利用勾股定理求出点A、B、C三点坐标,利用待定系数法即可解决问题.
(3)①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.②当PA⊥OA时,有一个点P满足条件.③当PO⊥OA时,有两个点P满足条件.
试题解析:解:(1)如图1中,连接EB、EC.
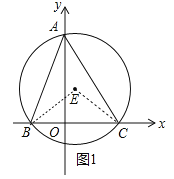
∵BC=OB+OC=5,∠BEC=2∠BC=90°,∴EB=EC=![]() ,∴⊙E的直径为
,∴⊙E的直径为![]() .
.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.
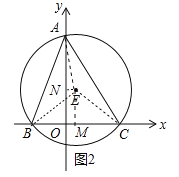
在Rt△EMC中,EM=ON=![]() =
= =
=![]() ,OM=NE=OC﹣CM=
,OM=NE=OC﹣CM=![]() ,在Rt△EN中,AN=
,在Rt△EN中,AN=![]() =
=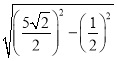 =
=![]() ,∴OA=AN+ON=6,∴A(0,6),B(﹣2,0),C(3,0),设抛物线的解析式为y=a(x+2)(x﹣3),把(0,6)的坐标代入得a=﹣1,∴抛物线的解析式为y=﹣x2+x+6.
,∴OA=AN+ON=6,∴A(0,6),B(﹣2,0),C(3,0),设抛物线的解析式为y=a(x+2)(x﹣3),把(0,6)的坐标代入得a=﹣1,∴抛物线的解析式为y=﹣x2+x+6.
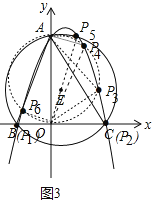
(3)如图3中,①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.
②当PA⊥OA时,有一个点P满足条件.
③当PO⊥OA时,有两个点P满足条件.
所以满足条件的点P有6个.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOE=120°,其中正确结论有_____;(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,连接AO,则图中一共有( )对全等三角形.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

(1)作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;
(2)点B1的坐标为__________,点C2的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 由
由![]() 绕点
绕点![]() 顺时针旋转得到,其中点
顺时针旋转得到,其中点![]() 与点
与点![]() 、点
、点![]() 与点
与点![]() 是对应点,连接
是对应点,连接![]() ,且
,且![]() 、
、![]() 、
、![]() 在同一条直线上,则
在同一条直线上,则![]() 的长为( )
的长为( )

A. 3 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电子产品共4件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品________件;
(2)如果从中任意取出2件,利用列表或树状图求取出2件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() .
.
(1)当m=2时,请解关于x、y的方程组![]() ;
;
(2)若关于x、y的方程组![]() 中,x为非负数、y为负数,
中,x为非负数、y为负数,
①试求m的取值范围;
②当m取何整数时,不等式3mx+2x>3m+2的解为x<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com