
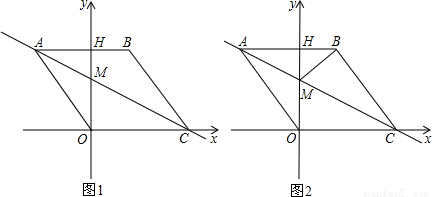
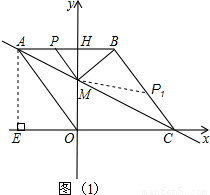
 解:(1)过点A作AE⊥x轴垂足为E,如图(1)
解:(1)过点A作AE⊥x轴垂足为E,如图(1)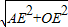 =5,
=5,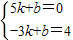 ,
,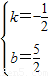 ,
, x+
x+ .(1分)
.(1分) ),
), ,
, =
= ,
, BP•MH=
BP•MH= (5-2t)•
(5-2t)• ,
, t+
t+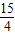 (0≤t<
(0≤t< ),2分
),2分 ,∠MOC=∠MBC=90°,
,∠MOC=∠MBC=90°, P1B•BM=
P1B•BM= (2t-5)
(2t-5) ,
, t-
t-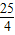 (
( <t≤5),2分
<t≤5),2分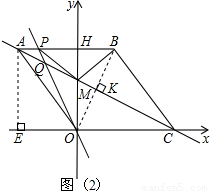
 ,(1分)
,(1分) =
=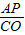 =
= ,
,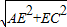 =
=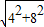 =4
=4 ,
, ,QC=
,QC=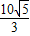 ,
,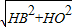 =
=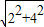 =2
=2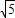 ,
,
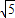 ,AK=KC=2
,AK=KC=2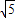 ,
,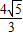 ,
,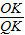 =
= ,(1分)
,(1分) =
=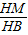 ,即
,即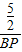 =
=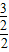 ,
,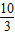 ,
,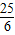 ,(1分)
,(1分)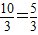 .
.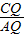 =
= ,
,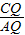 =
= ,
, AC=
AC= ,
,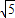 ,
,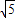 ,
,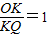 .(1分)
.(1分) 时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为 .
.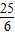 时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源:2010年云南省昆明市安宁市青龙学校中考数学模拟试卷(一)(解析版) 题型:选择题
 (k≠0)的图象上,则k的值是( )
(k≠0)的图象上,则k的值是( )

查看答案和解析>>
科目:初中数学 来源:2010年初中数学第一轮复习教学案例.4.4.反比例函数(解析版) 题型:选择题
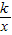 (k≠0)的图象上,则k的值是( )
(k≠0)的图象上,则k的值是( )

查看答案和解析>>
科目:初中数学 来源:2009年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:选择题
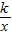 (k≠0)的图象上,则k的值是( )
(k≠0)的图象上,则k的值是( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com