
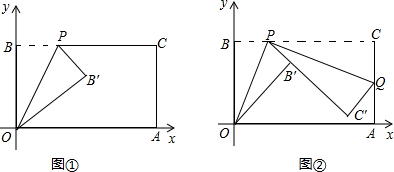
已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.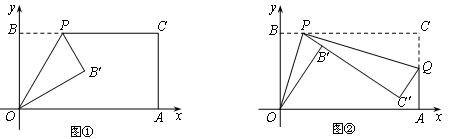
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
(Ⅰ)根据题意,∠OBP=90°,OB=6。
在Rt△OBP中,由∠BOP=30°,BP=t,得OP=2t。
∵OP2=OB2+BP2,即(2t)2=62+t2,解得:t1=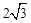 ,t2=-
,t2=-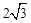 (舍去).
(舍去).
∴点P的坐标为(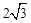 ,6)。
,6)。
(Ⅱ)∵△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,
∴△OB′P≌△OBP,△QC′P≌△QCP。
∴∠OPB′=∠OPB,∠QPC′=∠QPC。
∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°,∴∠OPB+∠QPC=90°。
∵∠BOP+∠OPB=90°,∴∠BOP=∠CPQ。
又∵∠OBP=∠C=90°,∴△OBP∽△PCQ。∴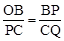 。
。
由题意设BP=t,AQ=m,BC=11,AC=6,则PC=11-t,CQ=6-m.
∴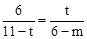 。∴
。∴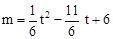 (0<t<11)。
(0<t<11)。
(Ⅲ)点P的坐标为(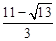 ,6)或(
,6)或(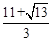 ,6)。
,6)。
解析


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,
别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,
别与x轴、y轴重合,折叠该纸,折痕与边OC交于点D,与对角线AC交于点M,查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的判定解答题(解析版) 题型:解答题
已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.

(Ⅰ)如图①,当∠BOP=30°时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com