
【题目】如图,在平面直角坐标系中,![]() 的半径为5,点A的坐标为(3,0),
的半径为5,点A的坐标为(3,0),![]() 与x轴相交于点B,C,交y轴正半轴于点D.
与x轴相交于点B,C,交y轴正半轴于点D.
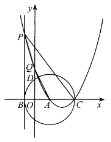
(1)求点B,D的坐标;
(2)过点B作![]() 的切线,与过点A,C的抛物线交于点P.抛物线交y轴正半轴于点Q.若P的纵坐标为t,四边形PQAC的面积为y.
的切线,与过点A,C的抛物线交于点P.抛物线交y轴正半轴于点Q.若P的纵坐标为t,四边形PQAC的面积为y.
①求y与t的函数关系式;
②若△PBO与△DOA相似,求![]() 取最小值时m的值.
取最小值时m的值.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②16
,②16
【解析】
(1)根据![]() 的半径为5,点A的坐标为(3,0),可求出点B的坐标,根据勾股定理可求出OD的长,即可求出点D的坐标;
的半径为5,点A的坐标为(3,0),可求出点B的坐标,根据勾股定理可求出OD的长,即可求出点D的坐标;
(2)①设过![]() ,
,![]() 的抛物线的解析式为
的抛物线的解析式为![]() .由其过点
.由其过点![]() ,可求得抛物线的解析式为:
,可求得抛物线的解析式为:![]() ,从而求出点Q的坐标及OQ的长,
,从而求出点Q的坐标及OQ的长,
由四边形PQAC的面积=![]() ,即可求出y与t的函数关系式;
,即可求出y与t的函数关系式;
②分两种情况:当![]() 和当
和当![]() ,根据相似三角形的性质列出关于t的方程,求出t的值,从而求出y的值,即可求出
,根据相似三角形的性质列出关于t的方程,求出t的值,从而求出y的值,即可求出![]() 取最小值时m的值.
取最小值时m的值.
(1)∵![]() 的半径为5,点A的坐标为(3,0),
的半径为5,点A的坐标为(3,0),![]() 与x轴相交于点B,C,
与x轴相交于点B,C,
∴点B的坐标为![]() ,点C的坐标为(8,0),
,点C的坐标为(8,0),
∵OA=3,AD=5,
∴![]() ,
,
∴D点坐标为(0,4),
(2)①设过![]() ,
,![]() 的抛物线的解析式为
的抛物线的解析式为![]() .
.
![]() 抛物线过点
抛物线过点![]() ,
,
∴![]() ,
,
![]() ,
,
∴抛物线的解析式为:![]() .
.
![]() ,即
,即![]() .
.
∴![]() ;
;
②若![]() ,
,
∴![]() ,即
,即![]() ,
,
可得![]() ,
,
∵![]() ,
,
∴![]() .
.
![]() .
.
当![]() 时,有最小值为
时,有最小值为![]() .
.
若![]() ,
,
∴![]() ,即
,即![]() ,
,
可得![]() ,
,
此时![]() .
.
![]() .
.
当![]() 时,有最小值为
时,有最小值为![]() .
.
![]() ,
,
![]() 取最小值时,
取最小值时,![]() 的值为16.
的值为16.


科目:初中数学 来源: 题型:
【题目】在2019年端午节前夕,某商场投入13800元资金购进甲、乙两种商品共500件,两种商品的成本价和销售价如下表所示:
商品 单价(元/件) | 成本价 | 销售价 |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进两种商品各多少件?
(2)这批商品全部销售完后,该商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
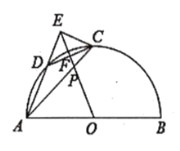
【题目】如图,在以![]() 为直径的半
为直径的半![]() 上有
上有![]() C,点
C,点![]() 在
在![]() 上,过圆心
上,过圆心![]() 作
作![]() 的于点
的于点![]() 的延长线交于点
的延长线交于点![]() ,连结
,连结![]() ,若
,若![]() .
.
![]() 试说明
试说明![]() ;
;
![]() 若
若![]() 的面积为
的面积为![]() 面积的
面积的![]() 倍,连接
倍,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值和
的值和![]() 的长:
的长:
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,直接写
,直接写![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
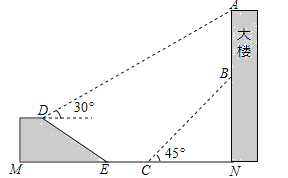
【题目】(12分)如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:![]() (即tan∠DEM=1:
(即tan∠DEM=1:![]() ),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:
),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).

(1)分数段在-----范围的人数最多;
(2)全校共有多少人参加比赛?
(3)学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,以AB为直径的⊙O交BC于点D,交AC于点E,点P是AB的延长线上一点,且∠PDB=![]() ∠A,连接DE,OE.
∠A,连接DE,OE.
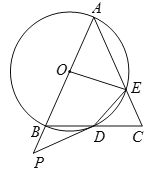
(1)求证:PD是⊙O的切线.
(2)填空:①当∠P的度数为______时,四边形OBDE是菱形;
②当∠BAC=45°时,△CDE的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象在第一象限交于
的图象在第一象限交于![]() 两点,一次函数的图象与
两点,一次函数的图象与![]() 轴交于点
轴交于点![]() .
.
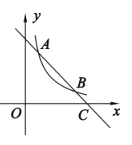
(1)求反比例函数和一次函数的表达式;
(2)当![]() 为何值时,
为何值时,![]() ?
?
(3)已知点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,在第一象限内交一次函数
轴的平行线,在第一象限内交一次函数![]() 的图象于点
的图象于点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() .结合函数图象直接写出当
.结合函数图象直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() .
.
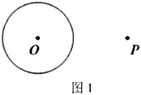
求作:过点![]() 作
作![]() 的切线.
的切线.
作法:如图2,
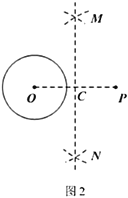
①连接![]() ;
;
②作线段![]() 的垂直平分线
的垂直平分线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 为半径作圆,交
为半径作圆,交![]() 于点
于点![]() 和
和![]() ;
;
④作直线![]() 和
和![]() .
.
则![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,
∵由作图可知![]() 是
是![]() 的直径,
的直径,
∴![]() (______)(填依据),
(______)(填依据),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半径,
的半径,
∴![]() ,
,![]() 就是
就是![]() 的切线(______)(填依据).
的切线(______)(填依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com