【题目】计算：|1﹣ 
|+3tan30°﹣（ ﹣5）0﹣（﹣ 
）﹣1 ．
【答案】解：原式= 
﹣1+3× 
﹣1﹣（﹣3）= ﹣1+ +3=2
【解析】先根据绝对值的意义，特殊锐角的三角函数值，零指数及负指数的意义分别化简，再按照有理数的计算方法进行计算。
【考点精析】根据题目的已知条件，利用零指数幂法则和整数指数幂的运算性质的相关知识可以得到问题的答案，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC中，∠BAD=∠EBC，AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ；
(2)若∠ABC=35°，EG∥AD，EH⊥BE，求∠HEG的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角梯形AOCD的边OC在x轴上，O为坐标原点，CD垂直于x轴，D（5，4），AD=2．若动点E、F同时从点O出发，E点沿折线OA→AD→DC运动，到达C点时停止；F点沿OC运动，到达C点时停止，它们运动的速度都是每秒1个单位长度．设E运动x秒时，△EOF的面积为y（平方单位），则y关于x的函数图象大致为（ ）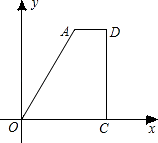
A.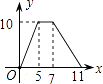
B.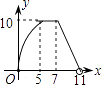
C.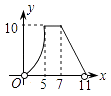
D.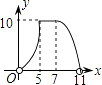
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F.
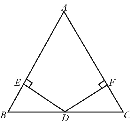
(1)求证；DE=DF；
(2)若∠A=90°，图中与DE相等的还有哪些线段?(不用说明理由)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB与CD相交于点O，OF，OD分别是∠AOE，∠BOE的平分线．
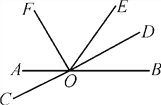
(1)写出∠DOE的补角；
(2)若∠BOE＝62°，求∠AOD和∠EOF的度数；
(3)试问射线OD与OF之间有什么特殊的位置关系？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ACB与△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D为AB边上的一点．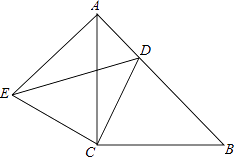
（1）求证：△BCD≌△ACE；
（2）若AE=12，DE=15，求AB的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
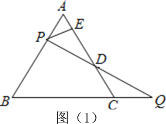
【题目】（1）老师在课上给出了这样一道题目：如图（1），等边△ABC边长为2，过AB边上一点P作PE⊥AC于E，Q为BC延长线上一点，且AP=CQ，连接PQ交AC于D，求DE的长.
小明同学经过认真思考后认为，可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.
（2）（类比探究）
老师引导同学继续研究：
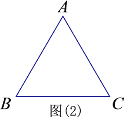
①等边△ABC边长为2，当P为BA的延长线上一点时,作PE⊥CA的延长线于点E ，Q为边BC上一点，且AP=CQ，连接PQ交AC于D.请你在图（2）中补全图形并求DE的长.
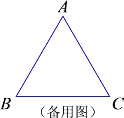
②已知等边△ABC，当P为AB的延长线上一点时,作PE⊥射线AC于点E， Q为哪一个（①BC边上；②BC的延长线上；③CB的延长线上）一点，且AP=CQ，连接PQ交直线AC于点D，能使得DE的长度保持不变.( 直接写出答案的编号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=﹣x2﹣2bx+c，当x＜2时，y的值随x的增大而增大，则实数b的取值范围是（ ）
A.b≥﹣1
B.b≤﹣1
C.b≥﹣2
D.b≤﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知点
，
，连接
，将向下平移5个单位得线段
，其中点
的对应点为点
．
（1）填空：点的坐标为_________，线段平移到扫过的面积为_______；
（2）若点
是
轴上的动点，连接
．
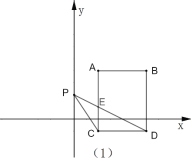
①如图（1），当点在轴正半轴时，线段
与线段
相交于点
，用等式表示三角形
的面积与三角形
的面积之间的关系，并说明理由；
②当将四边形
的面积分成
两部分时，求点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com