
����Ŀ����ͼ����A�͵�B�������϶�Ӧ�����ֱ�Ϊa��b���ң�a+6��2+|b��8|��0��
��1�����߶�AB�ij���
��2����C������������Ӧ����Ϊx����x�Ƿ���x��1��![]() x+1�Ľ⣬���߶�AB���Ƿ���ڵ�D��ʹ��AD+BD��
x+1�Ľ⣬���߶�AB���Ƿ���ڵ�D��ʹ��AD+BD��![]() CD�������ڣ��������D������������Ӧ�������������ڣ���˵�����ɣ�
CD�������ڣ��������D������������Ӧ�������������ڣ���˵�����ɣ�
��3���ڣ�2���������£��߶�AD��BC�ֱ���6����λ����/���5����λ����/����ٶ�ͬʱ�����˶����˶�ʱ��Ϊt�룬MΪ�߶�AD���е㣬NΪ�߶�BC���е㣬��MN��12����t��ֵ��

���𰸡���1��14����2�����߶�AB�ϴ��ڵ�D��ʹ��AD+BD��![]() CD����D������������Ӧ����Ϊ��2����3��t��3���27��.
CD����D������������Ӧ����Ϊ��2����3��t��3���27��.
��������
��1����ż�η��;���ֵ�ķǸ��Կɵ�a��b��ֵ���Ӷ��ɵ�AB��ֵ��
��2���ⷽ��x��1��![]() x+1���ɵõ�C������������Ӧ�����������߶�AB�ϴ��ڵ�D��ʹ��AD+BD��
x+1���ɵõ�C������������Ӧ�����������߶�AB�ϴ��ڵ�D��ʹ��AD+BD��![]() CD���ҵ�D������������Ӧ����Ϊy����������ݴ���ù���y��һԪһ�η��̣����y���ɣ�
CD���ҵ�D������������Ӧ����Ϊy����������ݴ���ù���y��һԪһ�η��̣����y���ɣ�
��3�������A��D��B��C�ĵ�������������Ӧ�������ٵ��˶�ǰM��N����������������Ӧ�������˶�t���M��N����������������Ӧ������Ȼ�����MN��12���������ۼ��㣬���tֵ���ɣ�
��1���ߣ�a+6��2��0��|b��8|��0��
�֡ߣ�a+6��2+|b��8|��0
�ࣨa+6��2��0��|b��8|��0
��a+6��0��8��b��0
��a����6��b��8
��AB��OA+OB��6+8��14��
��2���ⷽ��x��1��![]() x+1
x+1
�ã�x��14
���C������������Ӧ����Ϊ14��
�����߶�AB�ϴ��ڵ�D��ʹ��AD+BD��![]() CD���ҵ�D������������Ӧ����Ϊy����
CD���ҵ�D������������Ӧ����Ϊy����
AD��y+6��BD��8��y��CD��14��y
��y+6+��8��y����![]() ��14��y��
��14��y��
��ã�y����2
�����߶�AB�ϴ��ڵ�D��ʹ��AD+BD��![]() CD����D������������Ӧ����Ϊ��2��
CD����D������������Ӧ����Ϊ��2��
��3���ɣ�2���ã�A��D��B��C�ĵ�������������Ӧ�����ֱ�Ϊ��6��2��8��14.24��
���˶�ǰM��N����������������Ӧ�����ֱ�Ϊ��4��11
���˶�t���M��N����������������Ӧ�����ֱ�Ϊ��4+6t��11+5t
��MN��12
����߶�ADû�����߶�BCʱ�У�
��11+5t��������4+6t����12
��ã�t��3
���߶�AD���߶�BC���У�
����4t+6������11+5t����12
��ã�t��27
��������������t��3���27��ʱ�߶�MN��12��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������߹����ţ�������ˮλʱ��ˮ��![]() �Ŀ�Ϊ
�Ŀ�Ϊ![]() �ף����ŵ���ߵ�
�ף����ŵ���ߵ�![]() ��ˮ��
��ˮ��![]() �ľ���
�ľ���![]() Ϊ
Ϊ![]() �ף���
�ף���![]() ��
��![]() ���е㣬��ͼ���Ե�
���е㣬��ͼ���Ե�![]() Ϊԭ�㣬ֱ��
Ϊԭ�㣬ֱ��![]() Ϊ
Ϊ![]() �ᣬ����ֱ������ϵ
�ᣬ����ֱ������ϵ![]() .
.
��1����������ߵı���ʽ��
��2�����ˮ��![]() ����
����![]() �ף���
�ף���![]() ����ˮ��
����ˮ��![]() ����
����![]() �ڵ�
�ڵ�![]() ����࣬
����࣬
��ˮ�����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
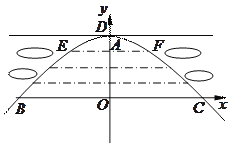
����Ŀ����ͼ���ڡ�ABC�У���ABC��90�㣬AC�Ĵ�ֱƽ���߷ֱ���AC��BC��AB���ӳ����ཻ�ڵ�D��E��F����O��EF�е㣬����BO���ӳ���G����GO��BO������EG��FG
��1�������ı���EBFG����״��˵�����ɣ�
��2����֤:BD��BG
��3����AB��BE��1ʱ����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
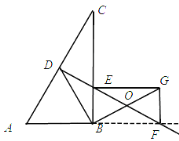
����Ŀ����֪��������ABCD�ı߳�Ϊ8����E��F�ֱ���AD��CD�ϣ�AE��DF��2��BE��AF�ཻ�ڵ�G����HΪBF���е㣬����GH����GH�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
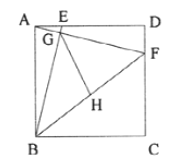
����Ŀ����ͼ����֪E��ABCD��BC�ߵ��е㣬����AE���ӳ�AE��DC���ӳ����ڵ�F.

(1)��֤����ABE�ա�FCE.
(2)����AC��BF������AEC=2��ABC����֤���ı���ABFCΪ���Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD����ƽ��ֱ������ϵ�У�����AD����x���ϣ�������߾���������ƽ�У�ֱ��l��y��x��3��x��ĸ�������ÿ��1����λ���ٶ�ƽ�ƣ���ƽ�ƵĹ����У���ֱ�߱�������ABCD�ı����صõ��߶γ�Ϊm��ƽ�Ƶ�ʱ��Ϊt���룩��m��t�ĺ���ͼ����ͼ2��ʾ����ͼ2��b��ֵΪ�� ��
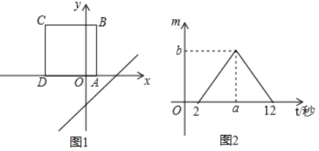
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F�ֱ��ڱ�AB��CD�ϣ���G��H�ڶԽ���AC�ϣ�AG��CH��BE��DF��
��1����֤���ı���EGFH��ƽ���ı��Σ�
��2����EG��EH��AB��8��BC��4����AE�ij���
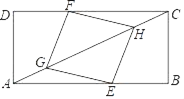
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ףԪ����ij�̳�����ǰ�Ŀյ����û������г�����ͼ��ʾ��ͼ������1��ͼ������10�����裬��2��ͼ������19�����裬�������˹���������ȥ.

��1����3��ͼ������______�����裬��4��ͼ������______�����裻
��2�������������ɣ������![]() ��ͼ���л���ĸ������ú�
��ͼ���л���ĸ������ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��3���Ƿ����ǡ����2026���������г��ľ����������ɵ�ͼ���������ڣ�˵�����ǵڼ���ͼ�����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ӹ������ó���ij�����´�����һ���ڼӹ�ij��������� 35000 �������ó���ӵ�����ƻ�ƽ��ÿ��ӹ� 5000 �������ڸ���ԭ��ÿ��ʵ�ʼӹ��ļ�����ÿ��ƻ��ӹ��ļ�������г��룬�ѳ������IJ��ֱַ���������������ʾ���±������ܼӹ�������������ļ�¼�����

��1�����ܵ�ǰ���칲�ӹ��˶��ټ���
��2�������ڼӹ�����һ��ȼӹ����ٵ�һ���ӹ��˶��ټ���
��3����֪�ó����������ʵ�мƼ������ƣ�ÿ�ӹ� 1 ���� 12 Ԫ������������������ÿ���ٽ� 8 Ԫ����û�����������ÿ��һ������ 8 Ԫ����ó������ܵ������룮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com