
【题目】对于平面直角坐标系xOy中的动点P和图形N,给出如下定义:如果Q为图形N上一个动点,P,Q两点间距离的最大值为dmax,P,Q两点间距离的最小值为dmin,我们把dmax+dmin的值叫点P和图形N间的“和距离”,记作d(P,图形N).
(1)如图1,正方形ABCD的中心为点O,A(3,3).
①点O到线段AB的“和距离”d(O,线段AB)=______;
②设该正方形与y轴交于点E和F,点P在线段EF上,d(P,正方形ABCD)=7,求点P的坐标.
(2)如图2,在(1)的条件下,过C,D两点作射线CD,连接AC,点M是射线CD上的一个动点,如果6![]() <d(M,线段AC)<6+3
<d(M,线段AC)<6+3![]() ,直接写出M点横坐标t取值范围.
,直接写出M点横坐标t取值范围.
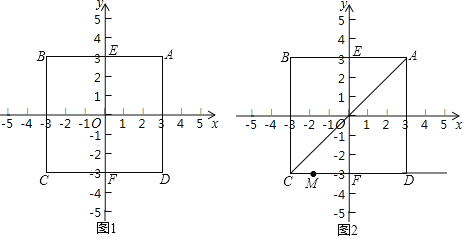
【答案】(1)①![]() ;②点P的坐标为(0,1)或(0,-1);(2)t取值范围是-3<t<3.
;②点P的坐标为(0,1)或(0,-1);(2)t取值范围是-3<t<3.
【解析】
(1)①根据“和距离“的定义计算:OE是两点间距离的最小值,OA是两点间的最大值,相加可得结论;
②分两种情况:P在y轴的正半轴和负半轴上,根据“和距离“的定义,并由d(P,正方形ABCD)=7,列方程计算即可得;
(2)分M在线段CD上和延长线上两种情况,利用“和距离”的定义列方程可得结论.
解:(1)①如图1,连接OA,

∵四边形ABCD是正方形,且A(3,3),
∴dmax+dmin=OE+OA=3+3![]() ,即d(O,线段AB)=3+3
,即d(O,线段AB)=3+3![]() ,
,
故答案为:3+3![]() ;
;
②设P(0,y),
∵d(P,正方形ABCD)=7,
∴dmax+dmin=7,
分两种情况:
∵E(0,3),F(0,-3),且P是线段EF上一个动点,
i)当P在x轴上方时,如图2,连接PC,
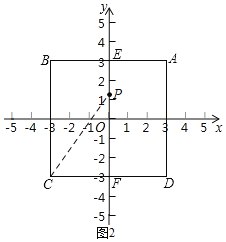
∴dmax+dmin=PE+PC=7,
3-y+![]() =7,
=7,
解得:y=1,
经检验,y=1是原方程的解,
∴P(0,1),
ii)当P在x轴的下方时,同理可得P(0,-1);
综上,点P的坐标为(0,1)或(0,-1);
(2)分两种情况:
①当-3≤t<3时,如图3,M在线段CD上,过M作MN⊥AC于N,连接AM,
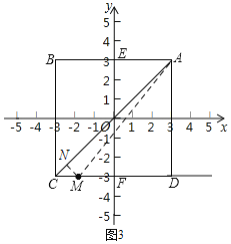
∵M点横坐标是t,
∴CM=t+3,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△CMN是等腰直角三角形,
∴MN=![]() (t+3),
(t+3),
∴d(M,线段AC)=MN+MA=![]() (t+3)+
(t+3)+![]() ,
,
②当t≥3时,如图4,M在线段CD的延长线上,过M作MN⊥AC于N,
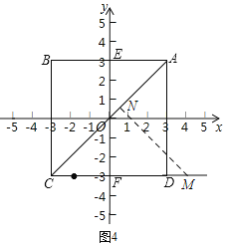
同理MN=![]() =
=![]() (t+3),
(t+3),
∴d(M,线段AC)=MN+CM=![]() (t+3)+t+3,
(t+3)+t+3,
∵在动点M从C到D方向上运动时,MN+MA越来越大,
∴![]() (t+3)+
(t+3)+![]() =6
=6![]() ,解得:t=-3,
,解得:t=-3,
![]() (t+3)+t+3=6+3
(t+3)+t+3=6+3![]() ,解得:t=3,
,解得:t=3,
∴M点横坐标t取值范围是-3<t<3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1所示,已知抛物线![]() 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.

(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,![]() =5:6?
=5:6?
(3)图2所示的抛物线是由![]() 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代第一部数学专著《九章算术》中有这样一道题:今有上禾7束,减去其中之实1斗,加下禾2束,则得实10斗.下禾8束,加实1斗和上禾2束,则得实10斗,问上禾、下禾1束得实多少?
译文为:今有上等禾7捆结出的粮食,减去1斗再加上2捆下等禾结出的粮食,共10斗;下等禾8捆结出的粮食,加上1斗和上等禾2捆结出的粮食,共10斗,问上等禾和下等禾1捆各能结出多少斗粮食?(斗为体积单位)
查看答案和解析>>
科目:初中数学 来源: 题型:
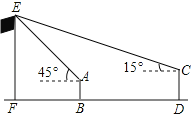
【题目】某校九(1)班开展数学活动,李明和张华两位同学合作用测角仪测量学校旗杆的高度,李明站在B点测得旗杆顶端E点的仰角为45°,张华站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知李明和张华相距(BD)30米,李明的身高(AB)1.6米,张华的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在⊙O上,AB为直径,BD与过点C的切线垂直于D,BD与⊙O交于点E.
(1)求证:BC平分∠DBA;
(2)如果cos∠ABD=![]() ,OA=2,求DE的长.
,OA=2,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
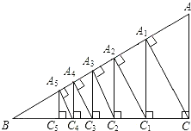
【题目】如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1;过CA1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2;…,这样一直做下去,得到一组线段A1C1,C2A2,…,则线段AnCn=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
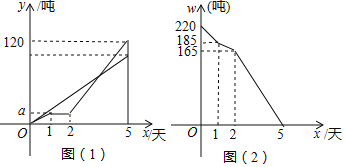
【题目】某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 吨,a= .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的交点(
(a≠0)的对称轴为直线x=1,与x轴的交点(![]() ,0),(
,0),(![]() ,0),且﹣1<
,0),且﹣1<![]() <0<
<0<![]() ,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则
,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则![]() =4a(c﹣n),其中正确的结论有( )个.
=4a(c﹣n),其中正确的结论有( )个.
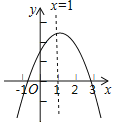
A. 5B. 4C. 3D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com