
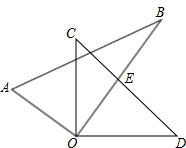
 将两个三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.
将两个三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.

科目:初中数学 来源: 题型:
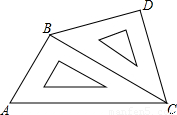
 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)| 22+22 |
| 2 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源:山东省菏泽市2010年初中学业水平考试数学试题 题型:022
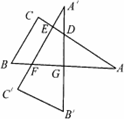
如图,三角板ABC的两直角边AC,BC的长分别为40 cm和30 cm,点G在斜边AB上,且BG=30 cm,将这个三角板以G为中心按逆时针旋转90°至△![]() 的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为________.
的位置,那么旋转前后两个三角板重叠部分(四边形EFGD)的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
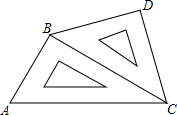 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)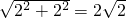
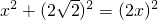
查看答案和解析>>
科目:初中数学 来源:2009-2010学年天津市河西区九年级(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com