
【题目】对于有理数a,b,定义两种新运算“※”与“◎”,规定: a※b=a2+2ab,a◎b=|a+ b|-|a- b|,例如,2※(- 1)=22+2×2×(-1)=0,(- 2) ※3=|-2+3|-| - 2-3|= -4.![]() b c
b c
(1)计算(- 3) ※2的值;
(2)若a, b在数轴上的位置如图所示,化简a◎b;
![]()
(3)若(-2) ※x=2◎(- 4)+ 3x,求x的值:
(4)对于任意有理数m,n,请你定义一种新运算“★” ,使得(-3) ★5 = 4,直接写出你定义的运算:m★n=_ (用含m,n的式子表示).
【答案】(1)-3;(2)-2b;(3)![]() ;(4)2(m+n)(答案不唯一).
;(4)2(m+n)(答案不唯一).
【解析】
(1)根据定义新运算公式计算即可;
(2)先判断a+ b和a- b的符号,然后根据绝对值的性质去绝对值化简即可;
(3)根据定义新运算公式解方程即可;
(4)根据已知等式,写出一种使等式成立的新运算即可.
解:(1)根据定义新运算公式可得:(- 3) ※2=(-3)2+2× (-3) ×2=-3;
(2)由数轴可知:a+ b<0,a-b<0
∴a◎b=|a+ b|-|a- b|
=- a-b+a-b
=-2b
(3)(-2) ※x=2◎(- 4)+ 3x
(-2)2+2× (-2) x=|2+(-4)|-|2-(-4)|+ 3x
4-4x=-4+ 3x
-7x=-8
解得:x=![]()
(4)∵(-3) ★5 = 4,而2×(-3+5)=4
∴可以定义m★n=2(m+n)
故答案为:2(m+n)(答案不唯一).


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
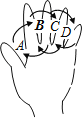
【题目】如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是_____;当字母C第201次出现时,恰好数到的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 分别是对角线BD上的两点,给出下列四个条件:①
分别是对角线BD上的两点,给出下列四个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中能判断四边形
.其中能判断四边形![]() 是平行四边形的个数是
是平行四边形的个数是

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用![]() 、
、![]() 表示,且
表示,且![]() .
.
(1)数轴上点A表示的数是 ,点B表示的数是
(2)若一动点P从点A出发,以3个单位长度/秒速度由A向B运动;动点Q从原点O出发,以1个单位长度/秒速度向B运动,点P、Q同时出发,点Q运动到B点时两点同时停止.设点Q运动时间为t秒.
①若P从A到B运动,则P点表示的数为 ,Q点表示的数为 .用含![]() 的式子表示)
的式子表示)
②当t为何值时,点P与点Q之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
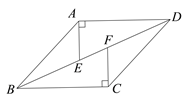
【题目】如图,在菱形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.
(1)证明:△ADE≌△CBF;
(2)连接AF、CE,四边形AECF是菱形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上任意一点,
边上任意一点,![]() 为
为![]() 边一动点,分别以
边一动点,分别以![]() 为边作等边三角形
为边作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() .
.

(1)试探索![]() 与
与![]() 的位置关系,并证明;
的位置关系,并证明;
(2)如图(2)当![]() 为
为![]() 延长线上任意一点时,(1)中的结论是否成立?请说明理由;
延长线上任意一点时,(1)中的结论是否成立?请说明理由;
(3)如图(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 为
为![]() 边一动点,分别以
边一动点,分别以![]() 为边作等腰三角形
为边作等腰三角形![]() 和等腰三角形
和等腰三角形![]() ,使得
,使得![]() ,连接
,连接![]() .要使(1)中的结论依然成立,还需要添加怎样的条件?为什么?
.要使(1)中的结论依然成立,还需要添加怎样的条件?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,有下列说法:
,有下列说法:
①如果当x≤1时![]() 随
随![]() 的增大而减小,则m≥1;
的增大而减小,则m≥1;
②如果它的图象与x轴的两交点的距离是4,则![]() ;
;
③如果将它的图象向左平移3个单位后的函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2013时的函数值相等,则当x=2014时的函数值为-3.
其中正确的说法是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两实数a与b,M=![]() +
+![]() ,N=2ab
,N=2ab
(1)请判断M与N的大小,并说明理由。
(2)请根据(1)的结论,求![]() +
+![]() +3的最小值(其中x,y均为正数)
+3的最小值(其中x,y均为正数)
(3)请判断![]() +
+![]() +
+![]() abacbc的正负性(a,b,c为互不相等的实数)
abacbc的正负性(a,b,c为互不相等的实数)
(4)若n为正整数,则(n+1)(n+4)(n2+5n)+4的值为某一个整数的平方,试说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com