
【题目】解答:(1)若一个多项式与![]() 的和是
的和是![]() ,求这个多项式.
,求这个多项式.
(2)已知![]() 和
和![]() 互余,且
互余,且![]() ,求
,求![]() 和
和![]() 的补角各是多少度?
的补角各是多少度?
【答案】(1)![]() ;(2)
;(2)![]() 的补角
的补角![]() ,
,![]() 的补角为
的补角为![]()
【解析】
(1)根据减法是加法的逆运算知,这个多项式可表示为:(3x-2)-(x2-2x+1),然后去括号,合并同类项求解;
(2)先根据∠α:∠β=1:5,设∠α=x,则∠β=5x,利用余角的性质求出∠α和∠β的度数,再根据补角的性质即可解答.
解:(1)(3x-2)-(x2-2x+1)
=3x-2-x2+2x-1
=-x2+5x-3.
∴这个多项式为-x2+5x-3;
(2)∵∠α:∠β=1:5,
∴设∠α=x°,则∠β=5x°,
∵∠α和∠β互余,
∴x+5x=90,解得x=15,
∴∠α=15°,∠β=5×15°=75°,
∴∠α的补角是180°-15°=165°,
∠β的补角是180°-75°=105°.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
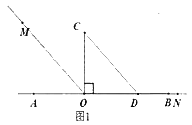
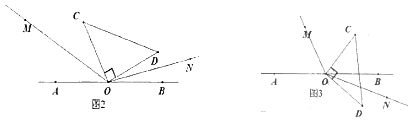
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
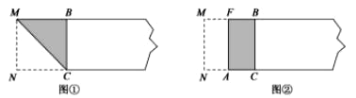
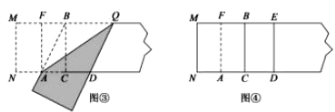
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
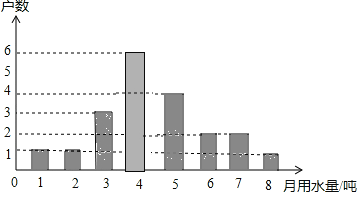
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店中销售水果时采用了三种组合搭配的方式进行销售,甲种搭配是:2千克A水果,4千克B水果;乙种搭配是:3千克A水果,8千克B水果,1千克C水果;丙种搭配是:2千克A水果,6千克B水果,1千克C水果;如果A水果每千克售价为2元,B水果每千克售价为1.2元,C水果每千克售价为10元,某天,商店采用三种组合搭配的方式进行销售后共得销售额441.2元,并且A水果销售额116元,那么C水果的销售额是______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③.

(1)图②有__________个三角形;图③有________个三角形;
(2)按上面的方法继续下去,第10个图有_________个三角形,第![]() 个图形中有_______个三角形.(用含
个图形中有_______个三角形.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
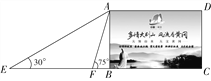
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图4所示).已知标语牌的高AB=5 m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上.求点E与点F之间的距离(计算结果精确到0.1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自![]() 月
月![]() 日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元 |
不超出 |
|
超出 |
|
超出 |
|
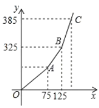
(1)若某用户![]() 月份用气量为
月份用气量为![]() ,交费多少元?
,交费多少元?
(2)调价后每月支付燃气费用![]() (单位:元)与每月用气量
(单位:元)与每月用气量![]() (单位:
(单位:![]() )的关系如图所示,求
)的关系如图所示,求![]() 与
与![]() 的解析式及
的解析式及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数对“
成立的一对有理数对“![]() ,
,![]() ”为“共生有理数对”,记为
”为“共生有理数对”,记为![]() .
.
(1)通过计算判断数对“-4,2”,“7,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若![]() 是“共生有理数对”,则“
是“共生有理数对”,则“![]() ,
,![]() ”______(填“是”或“不是”)共生有理数对”,并说明理由.
”______(填“是”或“不是”)共生有理数对”,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com