
分析 根据勾股定理求出斜边,根据直角三角形的外接圆的半径等于斜边的一半求出即可.
解答 解:由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∵△ACB是直角三角形,
∴△ABC的外接圆半径长为斜边的一半,即是$\frac{3\sqrt{5}}{2}$,
则△ABC的外接圆面积是:π($\frac{3\sqrt{5}}{2}$)2=$\frac{45}{4}$π.
故答案为:$\frac{45}{4}π$.
点评 本题考查了勾股定理和直角三角形的外接圆的应用,注意:直角三角形的外接圆的半径等于斜边的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 若△ABC中,a2=(b+c)(b-c),则△ABC是直角三角形 | |
| B. | 若△ABC中,a2+b2≠c2,则△ABC不是直角三角形 | |
| C. | 若△ABC中,a:b:c=13:5:12,则∠A=90° | |
| D. | 若△ABC中,a、b、c三边的长分别为n2-1、2n、n2+1(n>1),则△ABC是直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
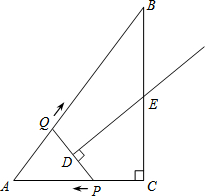 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交BC于点E.点P、Q同时出发,当点P到达点A时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有且只有1个 | B. | 有且只有2个 | C. | 不可能有3个 | D. | 有无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com