
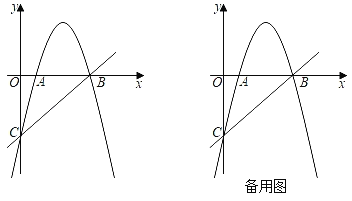
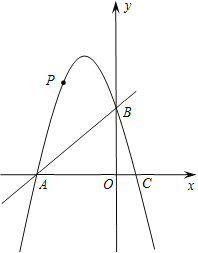
����Ŀ����ͼ��������y��ax2+6x+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x��5������B��C��
��1���������ߵĽ���ʽ��
��2������NΪ�������϶��㣬����NBA����OACʱ�����N�����꣬
��3������A��ֱ�߽�ֱ��BC�ڵ�M����AM��BCʱ������������һ����P�������B��C�غϣ�����ֱ��AM��ƽ���߽�ֱ��BC�ڵ�Q�����Ե�A��M��Q��PΪ������ı�����ƽ���ı��Σ����P�ĺ����꣮
���𰸡���1��y����x2+6x��5����2��N������Ϊ����4����45������3����P�ĺ�����Ϊ4��![]() ��
��![]() ��
��
��������
��1�������C��0����5����B��5��0��������y��ax2+6x+c��a��c��ֵ�����ɵó������
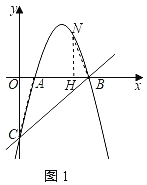
��2�����A��1��0�����ó�OA��1��OC��5����������������һ��N��NH��x���ڵ�H������AC��BN���ɡ�OAC����ǣ���N��ĺ�����С��5����֤��NBH����CAO���ó�![]() ����N������Ϊ��n����n2+6n��5������NH��|��n2+6n��5|��BH��|5��n|���ó�
����N������Ϊ��n����n2+6n��5������NH��|��n2+6n��5|��BH��|5��n|���ó� �����n��ֵ���ɵó������
�����n��ֵ���ɵó������
��3��֤����OCB����AMB��Ϊ����ֱ�������Σ���AM��![]() AB��
AB��![]() ����ƽ���ı��ε����ʵó�AM//PQ��PQ��AM��
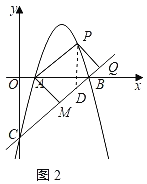
����ƽ���ı��ε����ʵó�AM//PQ��PQ��AM��![]() ���Ƴ�PQ��BC����PD��x�ύֱ��BC��D����ƽ���ߵ����ʵó���PDQ����OCB��45��������DPQ�ǵ���ֱ�������Σ��ó�PD��
���Ƴ�PQ��BC����PD��x�ύֱ��BC��D����ƽ���ߵ����ʵó���PDQ����OCB��45��������DPQ�ǵ���ֱ�������Σ��ó�PD��![]() PQ��4����P��m����m2+6m��5������D��m��m��5��������P��ֱ��BC�Ϸ�ʱ��PD����m2+5m��4���ⷽ�̼��ɣ�����P��ֱ��BC�·�ʱ��PD��m2��5m��4���ⷽ�̼��ɵó������
PQ��4����P��m����m2+6m��5������D��m��m��5��������P��ֱ��BC�Ϸ�ʱ��PD����m2+5m��4���ⷽ�̼��ɣ�����P��ֱ��BC�·�ʱ��PD��m2��5m��4���ⷽ�̼��ɵó������
�⣺��1����x��0ʱ��y��x��5����5��
��C��0����5����
��y��0ʱ��x��5��0��
��ã�x��5��
��B��5��0����
��B��5��0����C��0����5������y��ax2+6x+c�ã�![]() ��
��
��ã� ![]() ��
��
�������߽���ʽΪy����x2+6x��5��
��2���x2+6x��5��0����ã�x1��1��x2��5��
��A��1��0����
��C��0����5����
��OA��1��OC��5��
��������������һ��N��NH��x���ڵ�H������AC��BN����ͼ1��ʾ��
�ߡ�OAC����ǣ�
��N��ĺ�����С��5��
�ߡ�NBA����OAC����NHB��90������AOC��
���NBH����CAO��
��![]() ��
��
��N��������n����n2+6n��5����
��NH��|��n2+6n��5|��BH��|5��n|��
�� ��
��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��
��ã�n1��5����ȥ����n2��6����ȥ����
��![]() ʱ��
ʱ��
��ã�n1��5����ȥ����n2����4��
��n����4ʱ����n2+6n��5����45��
��N����4����45����
����������N����������4����45����
��3����A��1��0����B��5��0����C��0����5����
��AB��4����OCBΪ����ֱ�������Σ�
���OBC����OCB��45����
��AM��BC��
���AMBΪ����ֱ�������Σ�
��AM��![]() AB��
AB��![]() ��4��
��4��![]() ��
��
���Ե�A��M��Q��PΪ������ı�����ƽ���ı��Σ�
��AM//PQ��PQ��AM��![]() ��
��
��PQ��BC��
��PD��x�ύֱ��BC��D����ͼ2��ʾ��
���PDQ����OCB��45����
���DPQ�ǵ���ֱ�������Σ�
��PD��![]() PQ��
PQ��![]() ��
��
��P��m����m2+6m��5������D��m��m��5����
����P��ֱ��BC�Ϸ�ʱ��PD����m2+6m��5����m��5������m2+5m��4��
���m1��1����ȥ����m2��4��
����P��ֱ��BC�·�ʱ��PD��m��5������m2+6m��5����m2��5m��4��
��ã�m1��![]() ��m2��
��m2��![]() ��
��
������������P�ĺ�����Ϊ4��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������˾ȫ��Ա��ӻԾ������Я�ַ��ߣ������ѹ����������˾�����100000Ԫ����˾�����140000Ԫ�������Ǽס�������˾Ա����һ�ζԻ���
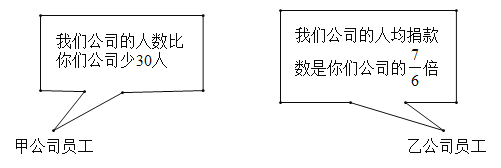
��1���ס�������˾���ж����ˣ�
��2���ּס�������˾��ͬʹ����ʾ���![]() ��
��![]() ���ַ������ʣ�
���ַ������ʣ�![]() �ַ�������ÿ��15000Ԫ��
�ַ�������ÿ��15000Ԫ��![]() �ַ�������ÿ��12000Ԫ��������
�ַ�������ÿ��12000Ԫ��������![]() �ַ������ʲ�����10�䣬��ǡ�ý�������꣬�м��ֹ���������Ƴ�����ע��
�ַ������ʲ�����10�䣬��ǡ�ý�������꣬�м��ֹ���������Ƴ�����ע��![]() ��
��![]() ���ַ������ʾ��蹺�����������ͣ���
���ַ������ʾ��蹺�����������ͣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����![]() ��
��![]() ������Ʒ���۳�2��
������Ʒ���۳�2��![]() ����Ʒ��3��
����Ʒ��3��![]() ����Ʒ��������Ϊ700Ԫ���۳�3��
����Ʒ��������Ϊ700Ԫ���۳�3��![]() ����Ʒ��5��
����Ʒ��5��![]() ����Ʒ��������Ϊ1100Ԫ��
����Ʒ��������Ϊ1100Ԫ��
��1����ÿ��![]() ����Ʒ��ÿ��
����Ʒ��ÿ��![]() ����Ʒ�۳�����������ֱ�Ϊ����Ԫ��
����Ʒ�۳�����������ֱ�Ϊ����Ԫ��
��2��������������![]() ��
��![]() ������Ʒ�ܿ����꣬�̳�������һ�ι���
������Ʒ�ܿ����꣬�̳�������һ�ι���![]() ��
��![]() ������Ʒ��34�����������34����Ʒȫ�����������������4000Ԫ����ô���̳������蹺�����ټ�
������Ʒ��34�����������34����Ʒȫ�����������������4000Ԫ����ô���̳������蹺�����ټ�![]() ����Ʒ��
����Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
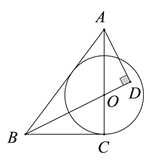
����Ŀ����ͼ����![]() �У�
�У�![]() Ϊ
Ϊ![]() ��һ�㣬��
��һ�㣬��![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶��Բ����
��Ϊ�뾶��Բ����![]() �����ڵ�
�����ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ,��
,��![]() .
.
��1����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ,��
,��![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������BAC�Ľ�ƽ����AD��BC����D����AB��ijһ��OΪԲ������O��ʹ��O������A�͵�D����AB�ߵ���һ������ΪE.
(1)�ж�ֱ��BC���O��λ�ù�ϵ����˵������;
(2)����O�İ뾶Ϊ4����B=30��.���߶�BD��BE���ӻ�DE��Χ�ɵ���Ӱ���ֵ�ͼ�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������۸��ܷ�����������Ӱ�죬�нϴ���ȵ�������Ϊ�˽�ij������ֳ���ܷ������������Ⱦ����������ִӸõ�����������ֳ���������ȡ�˲�����ֳ�������˵��飨�ѵ�������Ϊ�ĸ��ȼ���A�����dz����أ�B�������أ�C����һ�㣻D����û�и�Ⱦ�����������������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺
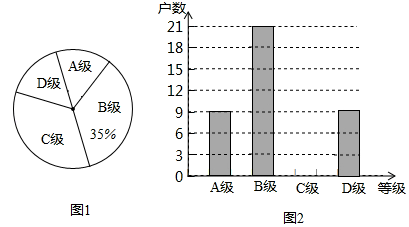
��1�����γ����������ֳ�����ܻ������� ������ͼ2����ͳ��ͼ����������
��2�����õ�����������ֳ����1500������dz����������ص���ֳ��һ���ж��ٻ���
��3��ij���е�λ���5��������ֳ�����ֱ��Ϊa��b��c��d��e�������ѡȡ��������һ�����ټ�ⲡ����������������б�����״ͼ�ķ������ѡ����ֳ��e�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
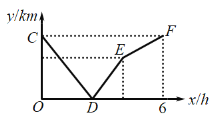
����Ŀ��A��B�������240 km��������A����40km/h���ٶ�����ǰ��B�أ�����B�غ�ֹͣ���ڼ׳�����ͬʱ���һ�����B����ͬһ��·����ǰ��A�أ�����A�غ�ֹͣ������֮���·��y��km�����������ʱ��x��h��֮��ĺ�����ϵ��ͼ�е�����![]() ��ʾ�����е�C��������
��ʾ�����е�C��������![]() ����D��������
����D��������![]() �����E��������__________��
�����E��������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���M������Ϊ��x1��y1������N������Ϊ��x2��y2������x1��x2��y1��y2����MNΪ�߹������Σ��������ε������Խ��߷ֱ�ƽ����x�ᣬy�ᣬ��Ƹ�����Ϊ�ߵġ��������Ρ���
��1����֪��A��2��0����B��0��2![]() ��������ABΪ�ߵġ��������Ρ�����С�ڽ�Ϊ�� ����
��������ABΪ�ߵġ��������Ρ�����С�ڽ�Ϊ�� ����
��2������C��1��2������D��ֱ��y=5�ϣ���CDΪ�ߵġ��������Ρ�Ϊ�����Σ���ֱ��CD ����ʽ��
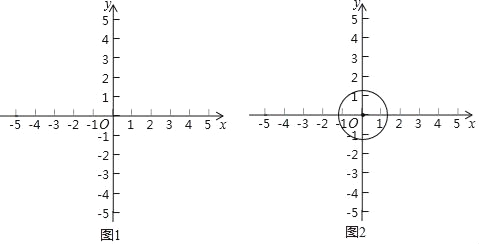
��3����O�İ뾶Ϊ![]() ����P������Ϊ��3��m����������O�ϴ���һ��Q��ʹ����QPΪ�ߵġ��������Ρ�Ϊ�����Σ���m��ȡֵ��Χ��
����P������Ϊ��3��m����������O�ϴ���һ��Q��ʹ����QPΪ�ߵġ��������Ρ�Ϊ�����Σ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x��4��x�ᡢy��ֱ���A��B���㣬������y=��x2��bx��c����A��B���㣬����x�ύ����һ��C����C��A���Ҳࣩ����P����������һ���㣮
��1���������ߵĽ���ʽ����C�����ꣻ
��2������P�ڵڶ������ڣ�����P��PD������D����AB�ڵ�E������P�˶���ʲôλ��ʱ���߶�PE�����ʱPE���ڶ��٣�
��3�����ƽ����x��Ķ�ֱ��l�������߽��ڵ�Q����ֱ��AB���ڵ�N����MΪOA���е㣬��ô�Ƿ����������ֱ��l��ʹ����MON�ǵ��������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com