
| A. | S32>S22>S12 | B. | S12=S22<S32 | C. | S12=S22>S32 | D. | S12=S22=S32 |
分析 根据第1组和第2组数据波动一样,第3组数据比前两组数据波动小,再根据方差的意义即可得出答案.
解答 解:观察第1组和第二2数据发现,发现两组数据一样稳定,
则S12=S22,
∵第3组数据比1、2组数据更稳定,
∴S12=S22>S32;
故选C.
点评 本题考查方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
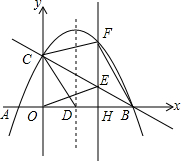 如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.
如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高(cm) | 180 | 186 | 188 | 192 | 208 |
| 人数(个) | 4 | 6 | 5 | 3 | 2 |
| A. | 186,186 | B. | 186,187 | C. | 208,188 | D. | 188,187 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com