
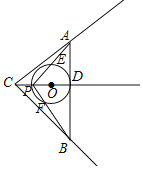
【题目】如图,在△ABC中,AB=7,BC=4![]() ,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
,∠ABC=45°,射线CD⊥AB于D,点P为射线CD上一动点,以PD为直径的⊙O交PA、PB分别为E、F,设CP=x.
(1)求sin∠ACD的值.
(2)在点P的整个运动过程中:
①当⊙O与射线CA相切时,求出所有满足条件时x的值;
②当x为何值时,四边形DEPF为矩形,并求出矩形DEPF的面积.
(3)如果将△ADC绕点D顺时针旋转150°,得△A′DC′,若点A′和点C′有且只有一个点在圆内,则x的取值范围是 .
【答案】(1)sin∠ACD=![]() ;(2)①x的值为x=1或x=10;②当x=4±2
;(2)①x的值为x=1或x=10;②当x=4±2![]() 时,四边形DEPF为矩形,矩形DEPF的面积为
时,四边形DEPF为矩形,矩形DEPF的面积为![]() ;(3)
;(3)![]() <x<7
<x<7
【解析】
(1)如图,在Rt△BCD中,BC=4![]() ,∠ABC=45°计算BD、CD,AD的长度,然后利用勾股定理求出AC的长度即可求解;
,∠ABC=45°计算BD、CD,AD的长度,然后利用勾股定理求出AC的长度即可求解;
(2)①⊙O与射线CA相切包括P在AB两侧两种情况,当P在AB左侧时,如图,sin∠ACD=![]() =
=![]() ,而CD=x+2r=4,可求x,同理当P在AB右侧时可解;
,而CD=x+2r=4,可求x,同理当P在AB右侧时可解;
②设圆的半径为r,四边形DEPF为矩形,包括P在AB两侧两种情况,当P在AB右侧时,如图设:PD=x﹣4=a,利用三角形APD的面积:ED=![]() 、DF=
、DF=![]() ,利用ED2=DF2可以求解,同理当当P在AB左侧的情况;
,利用ED2=DF2可以求解,同理当当P在AB左侧的情况;
(3)利用勾股定理分别求出PA′2,PC2,然后分r2=PA′2和 r2=PC′2两种情况,分别求解即可.
解:(1)在Rt△BCD中,BC=4![]() ,∠ABC=45°,
,∠ABC=45°,
则CD=4,BD=4,
![]() ,
,
∴AD=AB﹣BD=3,
![]()
sin∠ACD=![]() =
=![]() ;
;
(2)①⊙O与射线CA相切,包括P在AB两侧两种情况,
当P在AB左侧时,如下图,圆的半径为r,圆与AC相切于点H,
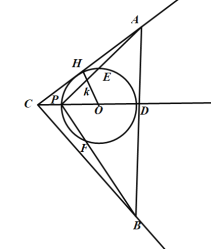
则在Rt△CHO中,OC=x+r,OH=r,sin∠ACD=![]() ,
,
sin∠ACD=![]() =
=![]() ,而CD=x+2r=4,
,而CD=x+2r=4,
解得:x=1,
同理当P在AB右侧时,求得x=4+6=10,
所有满足条件时x的值为x=1或x=10;
②设圆的半径为r,四边形DEPF为矩形,包括P在AB两侧两种情况,
当P在AB右侧时,原图的简图如下图,设∠ABP=∠DPE=α,
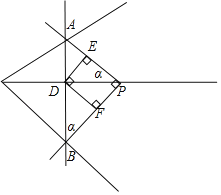
设:PD=x﹣4=a,
在Rt△ADP中,利用三角形APD的面积=![]() EDAP=
EDAP=![]() APPD,
APPD,
解得:ED=![]() ,
,
同理可得:DF=![]() ,PF2=a2﹣DF2,
,PF2=a2﹣DF2,
四边形DEPF为矩形,
∴ED2=DF2,
解得:a=2![]() ,x=4+2
,x=4+2![]() ,
,
则sinα=![]() ,cosα=
,cosα=![]() ,
,
S四边形DEPF=DPsinαcosα=![]() ,
,
同理当当P在AB左侧时,
此时PD=4﹣x=a,
经计算a=2![]() ,x=4﹣2
,x=4﹣2![]() ,
,
S四边形DEPF=DPsinαcosα=![]() ,
,
答:当x=4±2![]() 时,四边形DEPF为矩形,矩形DEPF的面积为
时,四边形DEPF为矩形,矩形DEPF的面积为![]() ;
;
(3)如下图,连接PA′、PC′,

在△PDA′中,AD′=3,PD=4﹣x,∠PDA=150°,
利用勾股定理得:PA′2=(![]() )2+(
)2+(![]() ﹣x)2=x2﹣11x+
﹣x)2=x2﹣11x+![]() ,
,
当r2=PA′2时,解得:x=7,
同理可得:PC2=32+16![]() ﹣(8+4
﹣(8+4![]() )x+x2,
)x+x2,
当r2=PC′2时,解得:x=![]() ,
,
∴x的取值范围为:![]() <x<7.
<x<7.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】感知定义
在一次数学活动课中,老师给出这样一个新定义:如果三角形的两个内角α与β满足α+2β=90°,那么我们称这样的三角形为“类直角三角形”.
尝试运用
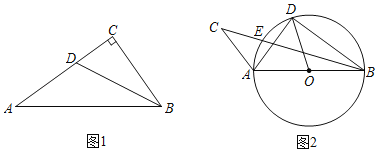
(1)如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,BD是∠ABC的平分线.
①证明△ABD是“类直角三角形”;
②试问在边AC上是否存在点E(异于点D),使得△ABE也是“类直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
类比拓展
(2)如图2,△ABD内接于⊙O,直径AB=10,弦AD=6,点E是弧AD上一动点(包括端点A,D),延长BE至点C,连结AC,且∠CAD=∠AOD,当△ABC是“类直角三角形”时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD与四边形CEFG都是矩形,点E,G分别在边CD,CB上,点F在AC上,AB=3,BC=4
(1)求![]() 的值;
的值;
(2)把矩形CEFG绕点C顺时针旋转到图②的位置,P为AF,BG的交点,连接CP
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)判断CP与AF的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.3.
(1)试求出纸箱中蓝色球的个数;
(2)小明向纸箱中再放进红色球若干个,小丽为了估计放入的红球的个数,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
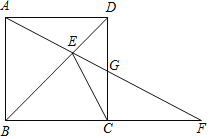
【题目】如图,在正方形ABCD中,点E是对角线BD上任意一点,连接AE并延长AE交BC的延长线于点F,交CD于点G.
(1)求证:∠DAE=∠DCE;
(2)若∠F=30°,DG=2,求CG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
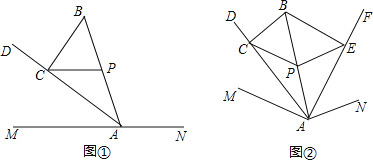
【题目】探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB的中点P作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.
应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结BC、BE.若∠MAN=150°,则∠CBE的大小为______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
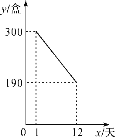
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com