
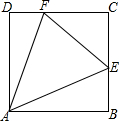
 如图,四边形ABCD为正方形(各边相等,各内角为直角),E是BC边上一点,F是CD上的一点.
如图,四边形ABCD为正方形(各边相等,各内角为直角),E是BC边上一点,F是CD上的一点.分析 (1)延长CF至G,使DG=BE,连接AG,由已知条件得出CE+CF+EF=CD+BC,得出DF+BE=EF,证出DF+DG=EF,即GF=EF,由SAS证明△ABE≌△ADG,得出AE=AG,∠BAE=∠DAG,证出∠EAG=90°,由SSS证明△AEF≌△AGF,得出∠EAF=∠GAF=$\frac{1}{2}$×90°=45°;
(2)由已知条件得出AB=AD=CD=BC=6,BE=BC-CE=3,由(1)得:△AEF的面积=△AGF的面积=△ABE的面积+△ADF的面积,即可得出答案.
解答 (1)证明:延长CF至G,使DG=BE,连接AG,如图所示: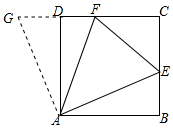
∵四边形ABCD是正方形,
∴∠BAD=∠ABE=∠ADF=90°,AB=BC=CD=AD,
∴∠ADG=90°,
∵△CFE的周长等于正方形ABCD的周长的一半,
∴CE+CF+EF=CD+BC,
∴DF+BE=EF,
∴DF+DG=EF,即GF=EF,
在△ABE和△ADG中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ABE=∠ADG=90°}&{\;}\\{BE=DG}&{\;}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∴∠EAG=90°,
在△AEF和△AGF中,$\left\{\begin{array}{l}{AE=AF}&{\;}\\{GF=EF}&{\;}\\{AF=AF}&{\;}\end{array}\right.$,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=$\frac{1}{2}$×90°=45°;
(2)解:∵DF=2,CF=4,CE=3,
∴AB=AD=CD=BC=2+4=6,BE=BC-CE=3,
由(1)得:△AEF的面积=△AGF的面积=△ABE的面积+△ADF的面积=$\frac{1}{2}$×6×3+$\frac{1}{2}$×6×2=15.
点评 本题考查了正方形的性质、全等三角形的判定与性质以及三角形面积的计算;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
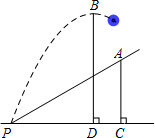 如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为10米时,球移动的水平距离PD为8米,已知山坡PA与水平方向PC的夹角为45°,AC⊥PC于点C,P、A两点相距10$\sqrt{2}$米.请你以P为原点,直线PC为x轴建立适当的平面直角坐标系解决下列问题.
如图,小明在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大高度BD为10米时,球移动的水平距离PD为8米,已知山坡PA与水平方向PC的夹角为45°,AC⊥PC于点C,P、A两点相距10$\sqrt{2}$米.请你以P为原点,直线PC为x轴建立适当的平面直角坐标系解决下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com