
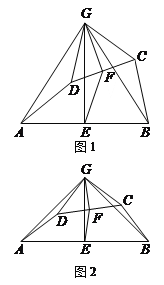
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
试题(1)根据线段垂直平分线上的点到线段两个端点的距离相等可得GA=GB,GD=GC.由“SAS”可判定△AGD≌△BGC根据全等三角形的对应边相等即可得AD=BC.(2)根据两边对应成比例且夹角相等的两个三角形相似可判定△AGB∽△DGC,再由相似三角形对应高的比等于相似比可得![]() ,再证得∠AGD=∠EGF,根据两边对应成比例且夹角相等的两个三角形相似即可判定△AGD∽△EGF.(3)如图1,延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH.由△AGD≌△BGC可知∠GAD=∠GBC.
,再证得∠AGD=∠EGF,根据两边对应成比例且夹角相等的两个三角形相似即可判定△AGD∽△EGF.(3)如图1,延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH.由△AGD≌△BGC可知∠GAD=∠GBC.
在△GAM和△HBM中,由∠GAD=∠GBC,∠GMA=∠HMB可证得∠AGB=∠AHB=90°,根据等腰三角形三线合一的性质可得∠AGE =45°,即可得出![]() 根据相似三角形对应边的比相等即可得
根据相似三角形对应边的比相等即可得![]()
试题解析:(1)证明:∵GE是AB的垂直平分线,∴GA=GB.同理GD=GC.
在△AGD和△BGC中,∵GA=GB,∠AGD=∠BGC,GD=GC, ∴△AGD≌△BGC.∴AD=BC.
(2) 证明:∵∠AGD=∠BGC, ∴∠AGB=∠DGC.
在△AGB和△DGC中,![]() ,∠AGB=∠DGC, ∴△AGB∽△DGC.
,∠AGB=∠DGC, ∴△AGB∽△DGC.
∴![]() ,又∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF.
,又∠AGE=∠DGF,∴∠AGD=∠EGF,∴△AGD∽△EGF.
(3)解:如图1,延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH.
由△AGD≌△BGC,知∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB.
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]()
又△AGD∽△EGF,
∴![]()
(本小题解法有多种,如可按图2、图3做辅助线求解,过程略)



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数![]() 的图象交于第二、四象限内的A,B两点,与
的图象交于第二、四象限内的A,B两点,与![]() 轴交于C点,过点A作AH⊥
轴交于C点,过点A作AH⊥![]() 轴,垂足为H,OH=3,tan∠AOH=
轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(
,点B的坐标为(![]() ,﹣2).
,﹣2).
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,点E是BC延长线上的一点,且BD=DE.点G是线段BC的中点,连结AG,交BD于点F,过点D作DH⊥BC,垂足为H.
(1)求证:△DCE为等腰三角形;
(2)若∠CDE=22.5°,DC=![]() ,求GH的长;
,求GH的长;
(3)探究线段CE,GH的数量关系并用等式表示,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小明想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为________;
(2)某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,用树状图或列表法求恰好选中《九章算术》和《孙子算经》的概率.(设《周髀算经》为![]() ,《九章算术》为
,《九章算术》为![]() ,《海岛算经》为
,《海岛算经》为![]() ,《孙子算经》为
,《孙子算经》为![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现问题)
如图1,已知![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为腰向
为腰向![]() 外作等腰直角
外作等腰直角![]() 、请你以
、请你以![]() 为直角顶点、
为直角顶点、![]() 为腰,向
为腰,向![]() 外作等腰直角
外作等腰直角![]() (不写作法,保留作图痕迹).连接
(不写作法,保留作图痕迹).连接![]() 、
、![]() .那么
.那么![]() 与
与![]() 的数量关系是________.
的数量关系是________.
(拓展探究)
如图2,已知![]() ,以
,以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() 、
、![]() ,试判断
,试判断![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.

(解决问题)
如图3,有一个四边形场地![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,记
中,记![]() ,
,![]() .
.
(1)如图![]() ,若
,若![]() 平分
平分![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的外角
的外角![]() 和
和![]() 的平分线,
的平分线,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数,用含
的度数,用含![]() 的代数式表示
的代数式表示![]() 的度数,并说明理由.
的度数,并说明理由.

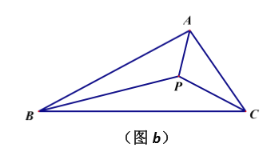
(2)如图![]() ,若点
,若点 ![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,![]() 于点
于点 ![]() , 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
, 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
![]() .
.
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边△ABC的边上的一个做匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到C为止,设运动时间为t,△ACP的面积为S,则S与t的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=90°,点D在边AB上,BE∥CD,AE⊥CD,垂足为F,且EF=2,点G在线段CF上,若∠GAF=45°,则△ACG的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com