
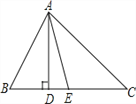
【题目】如图,在△ABC中,∠B=65°∠C=45°,AD是BC边上的高,AE是∠BAC的平线,求∠DAE的度数?
【答案】10 °
【解析】由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=25°,所以∠DAE=∠BAE-∠BAD=10°.
解:在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,
∴∠ADB=90°,
∵在△ABD中∠BAD=90°-∠B=25°,
∴∠DAE=∠BAE-∠BAD=10°.
“点睛”本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理,一定要熟稔于心.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
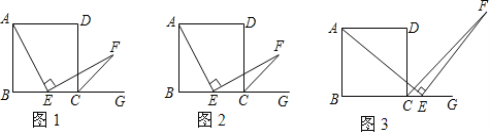
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:在AB上截取BM=BE,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如表所示:
用电量(度) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数分别是( )
A.180,160
B.160,180
C.160,160
D.180,180
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com