
【题目】在平面内,给定∠AOB=60°,及OB边上一点C,如图所示.到射线OA,OB距离相等的所有点组成图形G,线段OC的垂直平分线交图形G于点D,连接CD.
(1)依题意补全图形;直接写出∠DCO的度数;
(2)过点D作OD的垂线,交OA于点E,OB于点F.求证:CF=DE.

【答案】(1)见解析,30°;(2)见解析
【解析】
(1)根据角平分的判定定理可知图形G为∠AOC的平分线,是一条射线,据此补全图形;再根据垂直平分线和角平分线的性质转化角即可求出∠DCO的度数.
(2)通过中间线段DF进行转化可证得结论,即可先证明CF=DF,再证明DE=DF即可.
解:(1)根据角平分的判定定理可知图形G为∠AOC的平分线,是一条射线.补全图形如图1所示:

∠1,∠2,∠3,∠4,如图2所示,
∵OD是∠AOB的平分线,∠AOB =60°,
∴∠1 =∠2=30°,
又∵点D在OC的垂直平分线上,
∴CD=OD,
∴∠3 =∠2=30°.
即∠DCO=30°.
(2) 证明:∵EF⊥OD,
∴∠EDO =∠FDO =90°,
∴∠DFO =60°,又∠3=30°,
∴∠4 =30°,∴∠4 =∠3,
∴CF=DF,
又易得△OED≌△OFD,
∴DE=DF,
∴CF=DE.


科目:初中数学 来源: 题型:
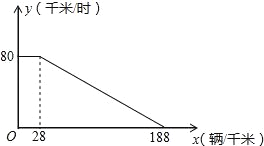
【题目】经研究表明,某市跨河大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,函数图象如图所示.
(1)求当28≤x≤188时,关于x的函数表达式;
(2)求车流量P(单位:辆/时)与车流密度x之间的函数关系式;(注:车流量是单位时间内通过观测点的车辆数,计算公式为:车流量=车流速度×车流密度)
(3)若车流速度V不低于50千米时,求当车流密度x为多少时,车流量P达到最大,并求出这一最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
⑴如图1,若∠BAC=60°,求证:△CEF是等边三角形.
⑵若∠BAC<60°.
①如图2,当点D在线段CB上移动时,判断△CEF为等腰三角形并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请你在图3中画出相应的图形并直接写出结论(不必证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=90°,∠ACB=30°,BC=![]() ,点D在边BC上,连接AD,在AD上方作等边三角形ADE,连接EC.
,点D在边BC上,连接AD,在AD上方作等边三角形ADE,连接EC.
(1)求证:DE=CE;
(2)若点D在BC延长线上,其他条件不变,直接写出DE,CE之间的数量关系(不必证明);
(3)当点D从点B出发沿着线段BC运动到点C时,求点E的运动路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
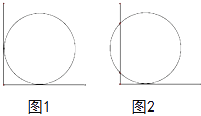
A. 25cm B. 30cm C. 50cm D. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
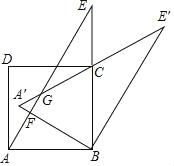
【题目】如图,把正方形ABCD和Rt△ABE重叠在一起,其中AB=2,∠BAE=60°,若把Rt△ABE绕直角顶点B按顺时针方向旋转,使斜边AE恰好经过正方形的顶点C,得到Rt△A′BE′,AE与A′B、A′E分别相交于点F,G,那么△ABE与△A′BE′的重叠部分(即四边形BCGF部分)的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是( )
![]() 弧AB的度数等于弧CD的度数;
弧AB的度数等于弧CD的度数;![]() 所对的圆心角等于弧CD所对的圆心角;
所对的圆心角等于弧CD所对的圆心角;
![]() 弧AB和弧CD是等弧;
弧AB和弧CD是等弧;![]() 弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.
弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com