
【题目】五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)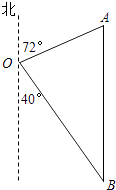
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△A′B′C′是△ABC 经过平移得到的,△ABC 中任意一点 P(x1,y1)平移后的对应点为 P′(x1+6,y1﹣5).
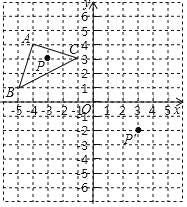
(1)请写出三角形 ABC 平移的过程;
(2)分别写出点 A′,B′,C′的坐标;
(3)画出平移后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
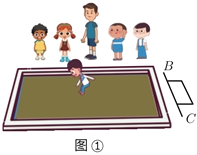
【题目】(数学实验)如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干个可以拼出一些长方形来解释某些等式.例如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.

(初步运用)
(1)仿照例子,图③可以解释为: ;
(2)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+3b)、(a+5b),不画图形,试通过计算说明需要C类卡片多少张;
(拓展运用)
若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积为2a2+5ab+3b2,通过操作你会发现拼成的长方形的长宽分别是 ,将2a2+5ab+3b2改写成几个整式积的形式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题.
(1)在正方形网格中,每个小正方形的边长均为1个单位长度,![]() 的三个顶点的位置如图所示,现将
的三个顶点的位置如图所示,现将![]() 平移,点
平移,点![]() 平移到点
平移到点![]() 的位置,
的位置,![]() 、
、![]() 点平移后的对应点分别是
点平移后的对应点分别是![]() 、
、![]() .
.
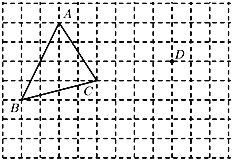
①画出平移后的![]() .
.
②连接![]() 、
、![]() ,则这两条线段之间的关系是__________.
,则这两条线段之间的关系是__________.
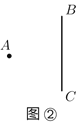
(2)如图①是体育课上跳远的场景,若运动员落地时后脚跟所在的点为![]() ,起跳线为
,起跳线为![]() ,请用图②说明怎样测量该运动员的跳远成绩,并说明其中的原因.
,请用图②说明怎样测量该运动员的跳远成绩,并说明其中的原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某航空公司托运行李的费用y(元)与行李的质量x(千克)之间的关系,由图可以看出:
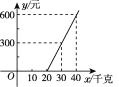
(1)当行李质量为30千克时,行李托运费是________元;
(2)当行李质量为________千克时,行李托运费是600元;
(3)每位旅客最多可以免费携带________千克的行李.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A坐标为(a,0),点B坐标为(b,2),点C坐标为(c,m),其中a、b、c满足方程组![]() .
.

(1)若a=2,则三角形AOB的面积为 ;
(2)若点B到y轴的距离是点C到y轴距离的2倍,求a的值;
(3)连接AB、AC、BC,若三角形ABC的面积小于等于9,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com