
【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
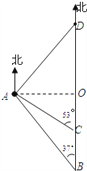
【答案】(1)货船与灯塔A之间的最短距离是36海里,B、C之间的距离是21海里.
(2)A、D之间的距离是60海里.
【解析】试题分析: (1)过点A作AO⊥BC,垂足为O.先解Rt△ACO中,求出CO=ACcos53°≈45×![]() =27,AO=ACsin53°≈45×
=27,AO=ACsin53°≈45×![]() =36.再解Rt△ABO,得到∠OAB=90°-37°=53°,BO=AOtan53°≈36×
=36.再解Rt△ABO,得到∠OAB=90°-37°=53°,BO=AOtan53°≈36×![]() =48,那么BC=BO-CO=48-27=21海里;
=48,那么BC=BO-CO=48-27=21海里;
(2)先根据路程=速度×时间求得BD=48×2=96,那么OD=BD-BO=96-48=48.然后在Rt△AOD中利用勾股定理求出AD=![]() =
=![]() =60海里.
=60海里.
试题解析:
(1)过点A作AO⊥BC,垂足为O.
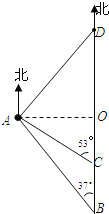
在Rt△ACO中,∵AC=45,∠ACO=53°,
∴CO=ACcos53°≈45×![]() =27,
=27,
AO=ACsin53°≈45×![]() =36.
=36.
在Rt△ABO中,∵AO=36,∠OAB=90°-37°=53°,
∴BO=AOtan53°≈36×![]() =48,
=48,
∴BC=BO-CO=48-27=21,
∴货船与灯塔A之间的最短距离是36海里,B、C之间的距离是21海里.
(2)∵BD=48×2=96,
∴OD=BD-BO=96-48=48.
在Rt△AOD中,∵∠AOD=90°,
∴AD=![]() =
=![]() =60,
=60,
∴A、D之间的距离是60海里.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.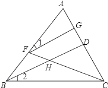
查看答案和解析>>
科目:初中数学 来源: 题型:
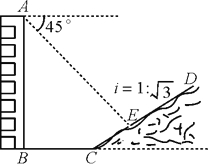
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶![]() ,山坡坡面上E点处有一休息亭,测
,山坡坡面上E点处有一休息亭,测
得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角
为45°,求楼房AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
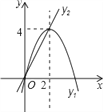
A. ③④ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,⊙C与y轴相切于D点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.
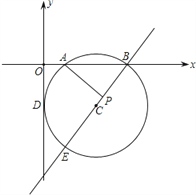
(1)求点C的坐标;
(2)连接BC并延长交⊙C于另一点E,若线段BE上有一点P,使得AB2=BPBE,能否推出AP⊥BE?请给出你的结论,并说明理由;
(3)在直线BE上是否存在点Q,使得AQ2=BQEQ?若存在,求出点Q的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下: ![]()
如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )
A. 汉城与纽约的时差为13小时 B. 北京与纽约的时差为13小时
C. 北京与纽约的时差为14小时 D. 北京与多伦多的时差为14小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .
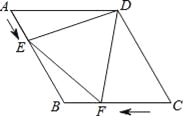
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com