
����Ŀ����֪��b����С������������a��b����![]() ��
��![]() ��0����ش����⣺
��0����ش����⣺
��1����ֱ��д��a��b��c��ֵ��
��2��������a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����M��A��B֮���һ�����㣬���Ӧ����Ϊm���뻯��![]() ����д��������̣���
����д��������̣���
��3���ڣ�1����2���������£���A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�BC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
![]()
���𰸡���1��-1��1��5����2���ٵ�m<0ʱ��|2m|=-2m���ڵ�m��0ʱ��|2m|=2m�����̼���������3��BC-AB��ֵ������ʱ��t�ı仯���仯����ֵ��2�����ɼ�����.
��������
��1���ȸ���b����С�������������b���ٸ���![]() ��
��![]() ��0���������a��c��ֵ��
��0���������a��c��ֵ��
��2���ȵó���A��C֮�䣨������A�㣩�����Ǹ�����0���ó�m��0���ڻ���|2m|���ɣ�
��3�������BC=3t+4��AB=3t+2���Ӷ��ó�BC-AB=2.
��1����b������������
��b=1
��![]() ��
��![]() ��0
��0
��a = -1��c=5
�ʴ�Ϊ��-1��1��5��
��2���ɣ�1��֪��a = -1��b=1��a��b������������Ӧ�ĵ�ֱ�ΪA��B��
�ٵ�m<0ʱ��|2m|=-2m��
�ڵ�m��0ʱ��|2m|=2m��
��3��BC-AB��ֵ������ʱ��t�ı仯���仯����ֵ��2���������£�
�ߵ�A��ÿ��һ����λ���ٶ������ƶ�����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������ƶ���
��BC=3t+4��AB=3t+2
��BC-AB=3t+4-��3t+2��=2



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı��� ACDE ��֤�����ɶ���ʱ�õ���һ��ͼ�Σ�a ��b ��c �� RtABC�� RtBED �ı߳�����֪![]() ����ʱ���ǰѹ��� x ������
����ʱ���ǰѹ��� x ������![]() ���η��̳�Ϊ����ϵһԪ���η�������
���η��̳�Ϊ����ϵһԪ���η�������

�����������⣺
(1)д��һ������ϵһԪ���η�������
(2)��֤������ x ������ϵһԪ���η�����![]() ������ʵ������
������ʵ������
(3)�� x 1������ϵһԪ���η����� ![]() ��һ���������ı��� ACDE ���ܳ���6
��һ���������ı��� ACDE ���ܳ���6![]() ����ABC �������
����ABC �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
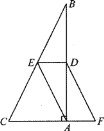
����Ŀ����ͼ��Rt��ABC����BAC=90�㣬��D��E�ֱ�Ϊ��AB��BC���е㣬��F��CA�ӳ����ϣ��ҡ�FDA=��B��
(1)��֤��AF=DE��
(2)��AC=3��BC=5�����ı���AEDF���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ൺ���˼��ų��˾����ʦ��ij�������Ӫ��ȫ���ڶ�������ļ���·�Ͻ��еģ�����涨��Ϊ��������Ϊ���������������г����![]() ��λ��ǧ��
��λ��ǧ��![]() ���£�
���£�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��1����ʦ���������Ŀ�ĵ�ʱ�����������ʱ�ij������ĸ���������������ض�Զ��
��2����ʦ���������繲�г�����ǧ�ף�
��3����ÿǧ����![]() ��������������ʦ�����˶������ͣ�
��������������ʦ�����˶������ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ���AD=BC����BD��AC����ƽ�֣����ı���ACED�����Σ�������ȷ�ĸ�����

A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�е�A������Ϊ(0��6)����B������Ϊ(��![]() ��5)������AOB��x������ƽ�Ƶõ���A��O��B������A�Ķ�Ӧ��A������ֱ��y����
��5)������AOB��x������ƽ�Ƶõ���A��O��B������A�Ķ�Ӧ��A������ֱ��y����![]() x�ϣ����B�Ķ�Ӧ��B��������Ϊ�� ��
x�ϣ����B�Ķ�Ӧ��B��������Ϊ�� ��
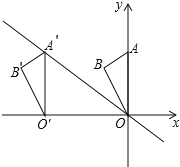
A.(��8��6)B.(��![]() ��5)C.(��
��5)C.(��![]() ��5)D.(��8��5)
��5)D.(��8��5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
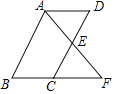
����Ŀ����ͼ����E��ƽ���ı���ABCD�ı�CD���е㣬�ӳ�AE��BC���ӳ����ڵ�F��
��1����֤����ADE�ա�FCE��
��2����AB��8��BC��5����EF�ij�Ϊ�� ��ʱ��AB��AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѳ�Ϊ�ҹ���ú�硢ˮ��֮��ĵ������Դ����������Ҫ�����˺�ҶƬ��ɣ���ͼ1����ͼ2�Ǵ�ͼ1������ƽ��ͼ��������վ��A��������˶���C��������55�㣬��HA����ˮƽǰ��43����ɽ��G������ɽ��B����������һҶƬ�������λ�ã���ʱ���ҶƬ�Ķ���D��D��C��H��ͬһֱ���ϣ���������45�㣮��֪ҶƬ�ij���Ϊ35�ף�������ҶƬ���Ӵ��ij��Ⱥ��Բ��ƣ���ɽ��BGΪ10�ף�BG��HG��CH��AH��������CH�ĸߣ����ο����ݣ�tan55���1.4��tan35���0.7��sin55���0.8��sin35���0.6��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽��һ�κ���![]() ��ͼ������ʱ���������·��֣�
��ͼ������ʱ���������·��֣�
��ϵ��![]() �����˺���ͼ����¶ȣ�
�����˺���ͼ����¶ȣ�![]() Խ����ͼ���¶�Խ��(Խ����
Խ����ͼ���¶�Խ��(Խ����![]() ��)��
��)��![]() ԽС��ͼ���¶�ԽС(Խ����
ԽС��ͼ���¶�ԽС(Խ����![]() ��)��
��)��
�ڳ�����![]() ������ͼ����
������ͼ����![]() ��Ľ��㣬������ͼ����
��Ľ��㣬������ͼ����![]() �ύ������ʼ��Ϊ
�ύ������ʼ��Ϊ![]() ��
��
�������Ϸ��֣����ǵó����ۣ��������һ�κ�����![]() ֵ��ͬ����ô����һ�κ�����ͼ��ƽ��.��֮�������ֱ��ƽ�У�������ֱ������Ӧ�ĺ�������ʽ��
ֵ��ͬ����ô����һ�κ�����ͼ��ƽ��.��֮�������ֱ��ƽ�У�������ֱ������Ӧ�ĺ�������ʽ��![]() ֵһ����ȣ��Ѻ���ͼ����
ֵһ����ȣ��Ѻ���ͼ����![]() ������(������) ƽ��
������(������) ƽ��![]() ����λ�� ϵ��
����λ�� ϵ��![]() ���ֲ��䣬 ����
���ֲ��䣬 ����![]() ��Ϊ
��Ϊ![]() (��
(��![]() ).�磺����
).�磺����![]() ��
��![]() ��ͼ����ƽ�У�����
��ͼ����ƽ�У�����![]() ��ͼ������ƽ��2����λ�����ú�������ʽΪ
��ͼ������ƽ��2����λ�����ú�������ʽΪ![]() ��
��
�ݴ˻ش��������⣺
(1) �Ѻ���![]() ��ͼ������ƽ��4����λ�����ú����ı���ʽΪ____��
��ͼ������ƽ��4����λ�����ú����ı���ʽΪ____��
(2)�Ѻ���![]() ��ͼ���� (�ϻ���)ƽ�� ����λ�ɵõ�����
��ͼ���� (�ϻ���)ƽ�� ����λ�ɵõ�����![]() ��ͼ��
��ͼ��
(3)��ֱ��![]() ������
������![]() ����ֱ��
����ֱ��![]() ƽ�У����ֱ��
ƽ�У����ֱ��![]() �ı���ʽ��
�ı���ʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com