
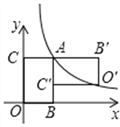
【题目】如图,矩形![]() 的顶点
的顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在反比例函数
在反比例函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象上,将矩形
)的图象上,将矩形![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到矩形
得到矩形![]() ,若点
,若点![]() 的对应点
的对应点![]() 恰好落在此反比例函数图象上,则
恰好落在此反比例函数图象上,则![]() 的值是__________.
的值是__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,若点
,若点![]() 是
是![]() 的重心.则以下结论:①线段
的重心.则以下结论:①线段![]() ,
,![]() ,
,![]() 是
是![]() 的三条角平分线;②
的三条角平分线;②![]() 的面积是
的面积是![]() 面积的一半;③图中与
面积的一半;③图中与![]() 面积相等的三角形有5个;④
面积相等的三角形有5个;④![]() 的面积是
的面积是![]() 面积的
面积的![]() .其中一定正确的结论有( )
.其中一定正确的结论有( )
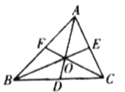
A.①②③B.②④C.③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
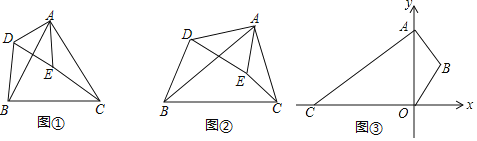
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买A、B两种型号电脑。已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同.
(1)求A、B两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,则最多可购买A种型号电脑多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
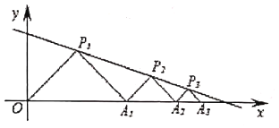
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,其直角顶点
,…都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,…均在直线
,…均在直线![]() 上.设
上.设![]() ,
,![]() ,
,![]() ,…的面积分别为
,…的面积分别为![]() ,
,![]() ,
,![]() ,…,根据图形所反映的规律,
,…,根据图形所反映的规律,![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
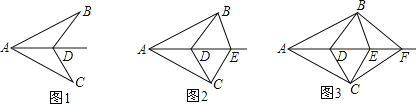
【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+![]() ∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-![]() ∠A.上述说法正确的个数是( )
∠A.上述说法正确的个数是( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com