
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
(1)见解析;(2)y=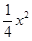 ﹣x+4.
﹣x+4.
(2)①当BP=1,MQ=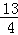 或BP=3,符合条件的平行四边形的个数有4个.②△PQC是直角三角形.
或BP=3,符合条件的平行四边形的个数有4个.②△PQC是直角三角形.
解析试题分析:(1)要证梯形ABCD是等腰梯形,只需证△AMB≌△DMC.
(2)由△BMP∽△CQP,可得到BP与CQ的关系,从而转化成y与x的函数关系式.
(3)先利用二次函数求最值,求出y取最小值时x的值和y的最小值,从而确定P、Q的位置,判断出△PQC的形状.
试题解析:
(1)证明:∵△MBC是等边三角形,
∴MB=MC,∠MBC=∠MCB=60°.
∵M是AD中点,
∴AM=MD.
∵AD∥BC,
∴∠AMB=∠MBC=60°,∠DMC=∠MCB=60°.
∴△AMB≌△DMC.
∴AB=DC.
∴梯形ABCD是等腰梯形.
(2)在等边△MBC中,MB=MC=BC=4,∠MBC=∠MCB=60°,∠MPQ=60°,
∴∠BMP+∠BPM=∠BPM+∠QPC=120°.
∴∠BMP=∠QPC.
∴△BPM∽△CQP.
∴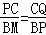 .
.
∵PC=x,MQ=y,
∴BP=4﹣x,QC=4﹣y.
∴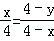 .
.
∴y=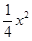 ﹣x+4.(8分)
﹣x+4.(8分)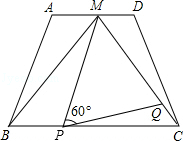
(3)①当BP=1时,则有BP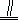 AM,BP
AM,BP MD,
MD,
则四边形ABPM为平行四边形,
∴MQ=y=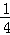 ×32﹣3+4=
×32﹣3+4=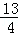 .(8分)
.(8分)
当BP=3时,则有PC AM,PC
AM,PC MD,
MD,
则四边形MPCD为平行四边形,
∴MQ=y=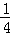 ×12﹣1+4=
×12﹣1+4=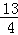 .(9分)
.(9分)
∴当BP=1,MQ=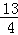 或BP=3,MQ=
或BP=3,MQ=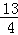 时,
时,
以P、M和A、B、C、D中的两个点为顶点的四边形是平行四边形.此时平行四边形有2个.
故符合条件的平行四边形的个数有4个.
②△PQC为直角三角形.
∵y=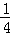 (x﹣2)2+3,
(x﹣2)2+3,
∴当y取最小值时,x=PC=2.
∴P是BC的中点,MP⊥BC,而∠MPQ=60°,
∴∠CPQ=30°,
∴∠PQC=90°.
∴△PQC是直角三角形.
考点:1.等腰梯形的判定;2.二次函数的最值;3.等边三角形的性质.


科目:初中数学 来源: 题型:解答题
理解与应用
小明在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第37页遇到这样一道题:
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)小明补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=60°,AC2= AB2+AB.BC.求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
观察计算:
当 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
当 ,
, 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
探究证明:
如图所示, 为圆O的内接三角形,
为圆O的内接三角形, 为直径,过C作
为直径,过C作 于D,设
于D,设 ,BD=b.
,BD=b.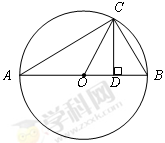
(1)分别用 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得出 与
与 的大小关系是:______________.
的大小关系是:______________.
实践应用:
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在矩形ABCD中,AB=4,AD=10.一把三角尺的直角顶点P在AD上滑动时(点P与A、D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
(1)证明△DPC∽△AEP;
(2)当∠CPD=30°时,求AE的长;
(3)是否存在这样的点P,使△DPC的周长等于△AEP周长的 倍?若存在,求出DP的长;若不存在,请说明理由.
倍?若存在,求出DP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?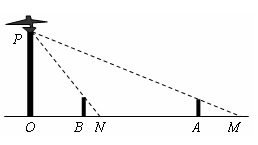
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直角△ABC中,∠C=90°,AB=2 ,sinB=
,sinB= ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
(1)求 、
、 的长;
的长;
(2)设 的长为
的长为 ,
, 的面积为
的面积为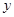 .当
.当 为何值时,
为何值时,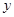 最大并求出最大值.
最大并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示,将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示,观察图2可知:与BC相等的线段是______,∠CAC′=______°。
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论.,
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H,若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135º,得到矩形EFGH(点E与O重合).
(1)若GH交y轴于点M,则∠FOM= ,OM= .
(2)将矩形EFGH沿y轴向上平移t个单位.
①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4 -2时,S与t之间的函数关系式.
-2时,S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com