
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=Љx2+2bxЉ3ЕФЖдГЦжсЮЊжБЯпx=2ЃЎ
ЃЈ1ЃЉЧѓbЕФжЕЃЛ
ЃЈ2ЃЉдкyжсЩЯгавЛЖЏЕуPЃЈ0ЃЌmЃЉЃЌЙ§ЕуPзїДЙжБyжсЕФжБЯпНЛХзЮяЯпгкЕуAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌЦфжаx1ЃМx2ЃЎ
ЂйЕБx2Љx1=3ЪБЃЌНсКЯКЏЪ§ЭМЯѓЃЌЧѓГіmЕФжЕЃЛ
ЂкАбжБЯпPBЯТЗНЕФКЏЪ§ЭМЯѓЃЌбижБЯпPBЯђЩЯЗелЃЌЭМЯѓЕФЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓWЃЌаТЭМЯѓWдк0ЁмxЁм5ЪБЃЌЉ4ЁмyЁм4ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ

ЁОД№АИЁПЃЈ1ЃЉb=2ЃЈ2ЃЉЂйЉ![]() ЂкЉ4ЁмmЁмЉ2
ЂкЉ4ЁмmЁмЉ2
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉРћгУЖўДЮКЏЪ§ЕФЖдГЦжсЙЋЪНМДПЩЧѓГіbжЕЃЛ
ЃЈ2ЃЉЂйИљОнЖўДЮКЏЪ§ЭМЯѓЕФжсЖдГЦадЃЌМДПЩЕУГіД№АИЃЛ
ЂкИљОнxЁЂyЕФШЁжЕЗЖЮЇЃЌМДПЩЕУmЕФШЁжЕЗЖЮЇ.
ЯъНтЃКЃЈ1ЃЉЁпХзЮяЯп![]() ЕФЖдГЦжсЮЊжБЯпx =2ЃЌ
ЕФЖдГЦжсЮЊжБЯпx =2ЃЌ
Ёрb=2ЃЎ
ЃЈ2ЃЉЂйЁрХзЮяЯпЕФБэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЁпAЃЈx1ЃЌyЃЉЃЌBЃЈx2ЃЌyЃЉЃЌ
ЁржБЯпABЦНааxжсЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁрAB=3ЃЎ
ЁпЖдГЦжсЮЊx =2ЃЌ

ЁрAC=![]() ЃЎ
ЃЎ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЎ
ЃЎ
ЂкЕБy=m=-4ЪБЃЌ0ЁмxЁм5ЪБЃЌ ![]() ЃЛ
ЃЛ
ЕБy=m=-2ЪБЃЌ0ЁмxЁм5ЪБЃЌ ![]() ЃЛ
ЃЛ
ЁрmЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁМЦЛЎЙКНјМзЁЂввСНжждЫЖЏаЌЃЌЦфжаМзЁЂввСНжждЫЖЏаЌЕФНјМлКЭЪлМлШчБэЃЈНјМлДѓгк50дЊЃЉ
дЫЖЏаЌМлИё | Мз | вв |
НјМлЃЈдЊ/ЫЋЃЉ | m | mЉ4 |
ЪлМлЃЈдЊ/ЫЋЃЉ | 160 | 150 |
вбжЊЃКгУ3000дЊЙКНјМзжждЫЖЏаЌЕФЪ§СПБШгУ2400дЊЙКНјввжждЫЖЏаЌЕФЪ§СПЖр5ЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉЩшИУЩЬГЁгІЙКНјМзжждЫЖЏаЌtЫЋЃЌСНжжаЌЙВ200ЫЋЃЌЩЬГЁЯњЪлЭъетХњаЌПЩЛёРћyдЊЃЌЧыЧѓГіyЙигкtЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЩЬГЁМЦЛЎдкЃЈ2ЃЉЕФЬѕМўЯТЃЌзмНјМлВЛЕЭгк19520дЊЃЌЧвВЛГЌЙ§19532дЊЃЌЮЪИУзЈТєЕъгаФФМИжжНјЛѕЗНАИЃП
ЃЈ4ЃЉЧѓИУзЈТєЕъвЊЛёЕУзюДѓРћШѓЕФНјЛѕЗНАИМАзюДѓРћШѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбЯТСаИїЪ§ЃК
Љ3.1ЃЌ3.1415ЃЌЉ![]() ЃЌ+31ЃЌ0.618ЃЌЉ
ЃЌ+31ЃЌ0.618ЃЌЉ![]() ЃЌ0ЃЌЉ1ЃЌЉЃЈЉ3ЃЉЃЌЬюдкЯргІЕФМЏКЯРя
ЃЌ0ЃЌЉ1ЃЌЉЃЈЉ3ЃЉЃЌЬюдкЯргІЕФМЏКЯРя
ЗжЪ§МЏКЯЃКЁЁ ЁЁЁЁ ЁЁЃЛ
ећЪ§МЏКЯЃКЁЁ ЁЁЁЁ ЁЁЃЛ
ЗЧИКећЪ§МЏКЯЃКЁЁ ЁЁЁЁ ЁЁЃЛ
е§гаРэЪ§МЏКЯЃКЁЁ ЁЁЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГЧјГѕЖўФъМЖЪ§бЇбЇПЦЦкФЉжЪСПМрПиЧщПіЃЌНјааСЫГщбљЕїВщЃЌЙ§ГЬШчЯТЃЌЧыНЋгаЙиЮЪЬтВЙГфЭъећЃЎ
ЪеМЏЪ§ОнЃКЫцЛњГщШЁМзввСНЫљбЇаЃЕФ20УћбЇЩњЕФЪ§бЇГЩМЈНјааЗжЮіЃК
Мз | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
вв | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
ећРэЁЂУшЪіЪ§ОнЃКАДШчЯТЪ§ОнЖЮећРэЁЂУшЪіетСНзщЪ§Он
ЗжЖЮ бЇаЃ | 30ЁмxЁм39 | 40ЁмxЁм49 | 50ЁмxЁм59 | 60ЁмxЁм69 | 70ЁмxЁм79 | 80ЁмxЁм89 | 90ЁмxЁм100 |
Мз | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
вв | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЗжЮіЪ§ОнЃКСНзщЪ§ОнЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЁЂЗНВюШчЯТБэЃК
ЭГМЦСП бЇаЃ | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю |
Мз | 81.85 | 88 | 91 | 268.43 |
вв | 81.95 | 86 | m | 115.25 |
ОЭГМЦЃЌБэИёжаmЕФжЕЪЧЁЁ ЁЁЃЎ
ЕУГіНсТлЃК
aШєМзбЇаЃга400УћГѕЖўбЇЩњЃЌЙРМЦетДЮПМЪдГЩМЈ80ЗжвдЩЯШЫЪ§ЮЊЁЁ ЁЁЃЎ
bПЩвдЭЦЖЯГіЁЁ ЁЁбЇаЃбЇЩњЕФЪ§бЇЫЎЦННЯИпЃЌРэгЩЮЊЁЁ ЁЁЃЎЃЈжСЩйДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
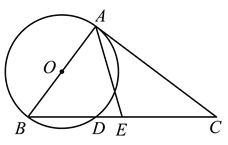
ЁОЬтФПЁПШчЭМЃЌвдABЮЊжБОЖзїЁбOЃЌЙ§ЕуAзїЁбOЕФЧаЯпACЃЌСЌНсBCЃЌНЛЁбOгкЕуDЃЌЕуEЪЧBCБпЕФжаЕуЃЌСЌНсAEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯAEB=2ЁЯCЃЛ
ЃЈ2ЃЉШєAB=6ЃЌ![]() ЃЌЧѓDEЕФГЄЃЎ
ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCЃЌBEЁЭACЃЌДЙзуЗжБ№ЮЊDЃЌEЃЌADгыBEЯрНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁзЁїBFDЃЛ
ЃЈ2ЃЉШєAC=BFЃЌЧѓЁЯABDЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§БШР§КЏЪ§y=kxОЙ§ЕуAЃЌЕуAдкЕкЫФЯѓЯоЃЌЙ§ЕуAзїAHЁЭxжсЃЌДЙзуЮЊЕуHЃЌЕуAЕФКсзјБъЮЊ3ЃЌЧвЁїAOHЕФУцЛ§ЮЊ3ЃЎ
ЃЈ1ЃЉЧѓе§БШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯФмЗёевЕНвЛЕуPЃЌЪЙЁїAOPЕФУцЛ§ЮЊ5ЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌPЮЊCDжаЕуЃЌЕуQЮЊABЩЯЕФЖЏЕуЃЈВЛгыAЃЌBжиКЯЃЉЃЎЙ§QзїQMЁЭPAгкMЃЌQNЁЭPBгкNЃЎЩшAQЕФГЄЖШЮЊxЃЌQMгыQNЕФГЄЖШКЭЮЊyЃЎдђФмБэЪОyгыxжЎМфЕФКЏЪ§ЙиЯЕЕФЭМЯѓДѓжТЪЧЃЈЁЁЃЉ
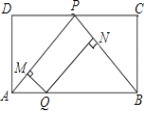

AЃЎ BЃЎ CЃЎ DЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com