练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．从-1，0，$\frac{22}{7}$，$\sqrt{2}$，$\root{3}{8}$中任取一个数，则取到的数是无理数的概率是$\frac{1}{5}$．

    分析 先找出无理数的个数，再根据概率公式即可得出答案．

    解答 解：∵在-1，0，$\frac{22}{7}$，$\sqrt{2}$，$\root{3}{8}$中，无理数有$\sqrt{2}$，共1个，
    ∴取到的数是无理数的概率是$\frac{1}{5}$；
    故答案为：$\frac{1}{5}$．

    点评 此题考查了概率公式和无理数的定义，找出无理数的个数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．点P（-a，b）关于y轴对称的点P′的坐标为（　　）
    A．（a，b）B．（a，-b）C．（-a，b）D．（-a，-b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若2amb4与$\frac{1}{2}$a3bn+2是同类项，则-m+n的值为-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．若x1，x2是方程x2-2x-3=0的两个根，则x1•x2=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．观察下列等式：
    第一层1+2=3
    第二层4+5+6=7+8
    第三层9+10+11+12=13+14+15
    第四层16+17+18+19+20=21+22+23+24
    …
    在上述的数字宝塔中，从上往下数，2017在第44层．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列命题正确的是（　　）
    A．a=$\sqrt{{a}^{2}}$=（$\sqrt{a}$）2B．若$\sqrt{{a}^{2}}$=a，则a=（$\sqrt{a}$）2C．（2$\sqrt{-7}$）2=28D．2$\sqrt{（-4）^{2}}$=-8

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知点A（-1，y1），B（3，y2）是双曲线y=$\frac{k}{x}$（k＜0）上的两点，则y1-y2＞0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

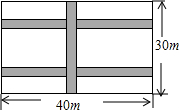    2．张明的父亲打算在院子里种上蔬菜．已知院子是东西长为40m，南北宽为30m的长方形，为了行走方便，要修筑同样宽的三条道路（如图），东西方向两条，南北方向一条．南北方道路垂直于东西道路，余下的部分分别种上蔬菜．若每条道路的宽为1m，求种蔬菜的土地的总面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．苏宁电器商场计划用9万元从生产厂家购进50台电视机．已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．
    （1）若苏宁电器商场同时购进两种不同型号的电视机共50台，用去9万元，请你研究一下商场的进货方案．
    （2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，你选择哪种方案？

    查看答案和解析>>

    同步练习册答案