
| A. | 6cm | B. | 9cm | C. | 3cm或6cm | D. | 1cm或9cm |
分析 分类讨论点C在AB上,点C在AB的延长线上,根据线段的中点的性质,可得BM、BN的长,根据线段的和差,可得答案.
解答 解:(1)点C在线段AB上,如:
点M是线段AB的中点,点N是线段BC的中点,
MB=$\frac{1}{2}$AB=5,BN=$\frac{1}{2}$CB=4,
MN=BM-BN=5-4=1cm;
(2)点C在线段AB的延长线上,如:

点M是线段AB的中点,点N是线段BC的中点,
MB=$\frac{1}{2}$AB=5,BN=$\frac{1}{2}$CB=4,
MN=MB+BN=5+4=9cm,
故选:D.
点评 本题考查了两点间的距离,分类讨论是解题关键,根据线段中点的性质,线段的和差,可得出答案.


科目:初中数学 来源: 题型:解答题
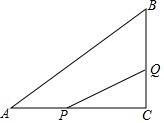 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
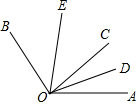 如图,∠AOB=120°,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )
如图,∠AOB=120°,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )| A. | ∠DOE的度数不能确定 | B. | ∠AOD=∠EOC | ||
| C. | ∠AOD+∠BOE=60° | D. | ∠BOE=2∠COD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
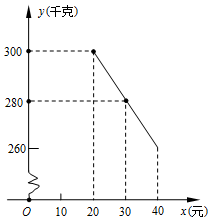 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com