
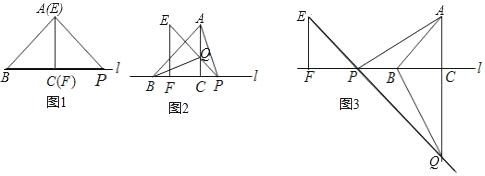
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
【答案】(1)AB=AP;AB⊥AP;(2)BQ=AP;BQ⊥AP;证明见解析;(3)成立,证明见解析.
【解析】
(1)根据图形就可以猜想出结论.
(2)要证BQ=AP,可以转化为证明Rt△BCQ≌Rt△ACP;要证明BQ⊥AP,可以证明∠QMA=90°,只要证出∠1=∠2,∠3=∠4,∠1+∠3=90°即可证出.
(3)类比(2)的证明就可以得到,结论仍成立.
(1)AB=AP;AB⊥AP;
∵AC⊥BC且AC=BC,
∴△ABC为等腰直角三角形,
∴∠BAC=∠ABC=![]() (180°﹣∠ACB)=45°,
(180°﹣∠ACB)=45°,
又∵△ABC与△EFP全等,
同理可证∠PEF=45°,
∴∠BAP=45°+45°=90°,
∴AB=AP且AB⊥AP;
(2)BQ=AP;BQ⊥AP.
证明:①由已知,得EF=FP,EF⊥FP,
∴∠EPF=45°.
又∵AC⊥BC,
∴∠CQP=∠CPQ=45°.
∴CQ=CP.
∵在Rt△BCQ和Rt△ACP中,
BC=AC,∠BCQ=∠ACP=90°,CQ=CP,
∴△BCQ≌△ACP(SAS),
∴BQ=AP.
②如图,延长BQ交AP于点M.
∵Rt△BCQ≌Rt△ACP,
∴∠1=∠2.
∵在Rt△BCQ中,∠1+∠3=90°,又∠3=∠4,
∴∠2+∠4=∠1+∠3=90°.
∴∠QMA=90°.
∴BQ⊥AP;
(3)成立.
①如图,∵∠EPF=45°,
∴∠CPQ=45°.
又∵AC⊥BC,
∴∠CQP=∠CPQ=45°.
∴CQ=CP.
∵在Rt△BCQ和Rt△ACP中,
BC=AC,CQ=CP,∠BCQ=∠ACP=90°,
∴Rt△BCQ≌Rt△ACP.
∴BQ=AP.
②如图③,延长QB交AP于点N,则∠PBN=∠CBQ.
∵Rt△BCQ≌Rt△ACP,
∴∠BQC=∠APC.
∵在Rt△BCQ中,∠BQC+∠CBQ=90°,
又∵∠CBQ=∠PBN,
∴∠APC+∠PBN=90°.
∴∠PNB=90°.
∴QB⊥AP.


科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c满足:a+c<0,ac>0,|b|=b,
(1)比较大小:a______0;b_____;c_____0;
(2)先去绝对值,再化简:|a﹣2b+c|﹣![]() +2|b﹣2c|的值.
+2|b﹣2c|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC = 110°,求∠EAN的度数;
(2)如图②,若∠BAC =80°,求∠EAN的度数;
(3)若∠BAC = α(α ≠ 90°),直接写出用α表示∠EAN大小的代数式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AD∥BC,点P为直线AB上一动点,点M在线段BC上,连接MP,![]() ,
,![]() ,
,![]() .
.
(1)如图1,当点P在线段AB上时,若![]() ,
,![]() =150°,则
=150°,则![]() =________°;
=________°;
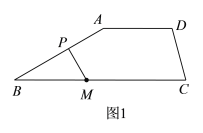
(2)如图2,当点P在AB的延长线上时,写出![]() ,
,![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;

(3)如图3,当点P在BA的延长线上时,请画出图形,直接写出![]() ,
,![]() 与
与![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究过程题)用直接开平方法解一元二次方程4(2x﹣1)2﹣25(x+1)2=0.
解:移项得4(2x﹣1)2=25(x+1)2,①
直接开平方得2(2x﹣1)=5(x+1),②
∴x=﹣7. ③
上述解题过程,有无错误如有,错在第_____步,原因是_____,请写出正确的解答过程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三名打字员承担一项打字任务,已知如下信息:
信息一:甲单独完成任务所需时间比乙单独完成任务所需时间多5小时;
信息二:甲4小时完成的工作量与乙3小时完成的工作量相等;
信息三:丙的工作效率是甲的工作效率的2倍.
如果每小时只安排1名打字员,那么按照甲、乙、丙的顺序至完成工作任务,共需( )
A.![]() 小时B.
小时B.![]() 小时C.
小时C.![]() 小时D.
小时D.![]() 小时
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com