
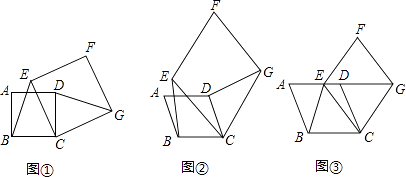
【题目】【感知】如图①,四边形ABCD、CEFG均为正方形,可知BE=DG.
【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F,求证:BE=DG.
【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上,若AE=2ED,∠A=∠F,△EBC的面积为6,则菱形CEFG的面积为 . 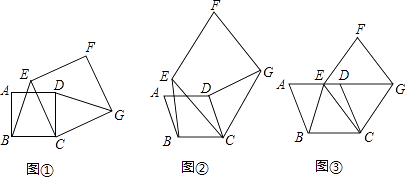
【答案】16
【解析】解:拓展:∵四边形ABCD、四边形CEFG均为菱形,
∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.
∵∠A=∠F,
∴∠BCD=∠ECG.
∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,
即∠BCE=∠DCG.
在△BCE和△DCG中,
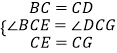 ,
,
∴△BCE≌△DCG(SAS),
∴BE=DG.
应用:∵四边形ABCD为菱形,
∴AD∥BC,
∵△BCE≌△DCG,
∴S△ABE+S△CDE=S△BEC=S△CDG=6,
∵AE=2ED,
∴S△CDE= ![]() ×6=2,
×6=2,
∴S△ECG=S△CDE+S△CDG=8,
∴S菱形CEFG=2S△ECG=16.
故答案为16.
拓展:由四边形ABCD、四边形CEFG均为菱形,利用SAS易证得△BCE≌△DCG,则可得BE=DG;
应用:由AD∥BC,△BCE≌△DCG,可得S△ABE+S△CDE=S△BEC=S△CDG=6,又由AE=2ED,可求得△CDE的面积,继而求得答案.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】某超市购进一批文具袋,每个进价为8元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元) | 11 | 12 | 13 | 14 | … |
销售数量y(个) | 34 | 32 | 30 | 28 | … |
备注:物价局规定,每个文具袋的售价不低于8元且不高于18元 | |||||
(1)请你根据表中信息判断y是x的什么函数?求出其函数关系式,并写出自变量取值范围.
(2)有一天文具袋的销售单价为17元,不计其他因素,求该天销售文具袋的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.如果两个角相等,那么这两个角是对顶角
B.两直线被第三条直线所截,所得的内错角相等
C.两平行线被第三条直线所截,同位角相等
D.经过一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若自然数n使得作竖式加法n+(n+1)+(n+2)均不产生进位现象,则称n为“可连数”,例如32是“可连数”,因为32+33+34不产生进位现象;23不是“可连数”,因为23+24+25产生了进位现象,那么小于10的“可连数”的个数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作ABDE,连结AD、EC. 
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?(直接写出满足的条件即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com