【题目】如图，在
中，
，
，AD是的中线，AE是
的角平分线，
交AE的延长线于点F，则DF的长为________．
【答案】4
【解析】
根据等腰三角形三线合一的性质可得到AD⊥BC，∠BAD=∠CAD，从而可得到∠BAD=60°，∠ADB=90°，再根据角平分线的性质即可得到∠DAE=∠EAB=30°，从而可推出AD=DF，根据直角三角形30度角的性质即可求得AD的长，即得到了DF的长．
解：∵△ABC是等腰三角形，D为底边的中点，
∴AD⊥BC，∠BAD=∠CAD，
∵∠BAC=120°，
∴∠BAD=60°，∠ADB=90°，
∵AE是∠BAD的角平分线，
∴∠DAE=∠EAB=30°．
∵DF∥AB，
∴∠F=∠BAE=30°．
∴∠DAF=∠F=30°，
∴AD=DF．
∵AB=8，∠B=30°，
∴AD=4，
∴DF=4
故选：C．
寒假创新型自主学习第三学期寒假衔接系列答案科目：初中数学 来源： 题型：
【题目】甲、乙两人以各自的交通工具、相同路线，前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙前往目的地所走的路程S（km）随时间t（分）变化的函数图象．以下说法：①乙比甲提前12分钟到达；②乙走了8km后遇到甲；③乙出发6分钟后追上甲；④甲走了28分钟时，甲乙相距3km．其中正确的是（ ）
A. 只有① B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABO中，斜边AB=1，若OC∥BA，∠AOC=36°，则（ ）
A. 点B到AO的距离为sin54°
B. 点A到OC的距离为sin36°sin54°
C. 点B到AO的距离为tan36°
D. 点A到OC的距离为cos36°sin54°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知二次函数y=ax2+
x+c（a≠0）的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．
（1）请直接写出二次函数y=ax2+x+c的表达式；
（2）判断△ABC的形状，并说明理由；
（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请写出此时点N的坐标；
（4）如图2，若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）
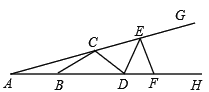
A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，动点P在∠ABC的平分线BD上，动点M在BC边上，若BC=3，∠ABC=45°，则PM+PC的最小值是( )
A. 2 B. 
C. 
D. 3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等腰Rt△ABC中，∠ACB=90°，AB=4，点E为AB的中点．以AE为边作等边△ADE（点D与点C分别在AB的异侧），连接CD．则△ACD的面积为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
