
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
【答案】(1)该小区有250套80平方米住宅;(2)![]() 的值为50.
的值为50.
【解析】
(1)设该小区有x套80平方米住宅,则50平方米住宅有2x套,根据物管费90000元,可列方程求解;(2)50平方米住宅有500×40%=200户参与活动一,80平方米住宅有250×20%=50户参与活动一;50平方米住宅每户所交物管费为100(1-![]() a%)元,有200(1+2a%)户参与活动二;80平方米住宅每户所交物管费为160(1-
a%)元,有200(1+2a%)户参与活动二;80平方米住宅每户所交物管费为160(1-![]() a%)元,有50(1+6a%)户参与活动二.根据参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
a%)元,有50(1+6a%)户参与活动二.根据参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() a%,列出方程求解即可.
a%,列出方程求解即可.
(1)解:设该小区有x套80平方米住宅,则50平方米住宅有2x套.
由题意得知:![]()
解得![]()
答:该小区有250套80平方米住宅.
(2)
参与活动一:
50平方米住宅每户所交物管费为100元,有![]() 套参与活动一,
套参与活动一,
80平方米住宅每户所交物管费为160元,有![]() 套参与活动二,
套参与活动二,
参与活动二:
50平方米住宅每户所交物管费为![]() 元,有
元,有![]() 套参与活动一;
套参与活动一;
80平方米住宅每户所交物管费为![]() 元,有50
元,有50![]() 套参与活动二;
套参与活动二;
由题意得:![]()
![]()
令![]() .
.
化简得:![]() .
.
解得:![]() (舍去),
(舍去),![]()
![]()
![]() (舍去)
(舍去)
答:![]() 的值为50.
的值为50.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc<0;②a﹣b+c>0;③2a+b=0;④b2﹣4ac<0;正确的有( )个.
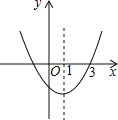
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线与直线y=x+3分别交于x轴和y轴上同一点,交点分别是点A和点C,且抛物线的对称轴为直线x=-2.
(1)求出抛物线与x轴的两个交点A、B的坐标.
(2)试确定抛物线的解析式.
(3)观察图象,请直接写出二次函数值小于一次函数值的自变量x的取值范围.
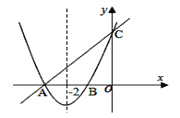
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在矩形 ABCD 中 AB=8,BC=6,AE=BE,点 F 为边 BC 上任意一点,将BEF 沿着 EF 翻折,点 B 为点 B 的对应点,则当BCD 的面积最小时BCF 的面积为( )

A.4B.6C.4.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙D于点D,交AC于点E,连接AD,BD,CD若AB=10,cos∠ABC=![]() ,则tan∠DBC的值是( )
,则tan∠DBC的值是( )
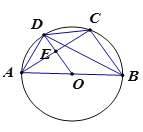
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用
,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用![]() 表示
表示
![]() 求这条绳子最低点离地面的距离;
求这条绳子最低点离地面的距离;
![]() 现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑
现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑![]() 如图
如图![]() ,已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.
,已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.
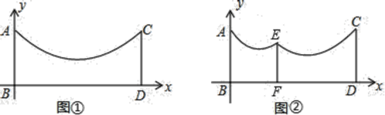
查看答案和解析>>
科目:初中数学 来源: 题型:
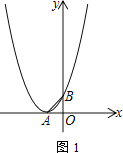
【题目】已知抛物线顶点A在x轴负半轴上,与y轴交于点B,OB=1,△OAB为等腰直角三角形
(1)求抛物线的解析式
(2)若点C在抛物线上,若△ABC为直角三角形,求点C的坐标
(3)已知直线DE过点(-1,-4),交抛物线于点D、E,过D作DF∥x轴,交抛物线于点F,求证:直线EF经过一个定点,并求定点的坐标

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com