
【题目】在同一平面内,若有![]() 条直线,则最多有______个交点;若
条直线,则最多有______个交点;若![]() 条直线中恰好有且只有
条直线中恰好有且只有![]() 条直线互相平行,则这
条直线互相平行,则这![]() 条直线最多有_____个交点(用含有
条直线最多有_____个交点(用含有![]() 的式子表示).
的式子表示).
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】已知直角坐标平面内两点A(-2,-3)、B(3,-3),将点B向上平移5个单位到达点C,求:

(1)A、B两点间的距离;
(2)写出点C的坐标;
(3)四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写理由:
已知:如图,ABC是直线,∠1=115°,∠D=65°.
求证:AB∥DE.

证明:∵ABC是一直线,(已知)
∴∠1+∠2=180°( )
∵∠1=115°(已知)
∴∠2=65°
又∵∠D=65°(已知)
∴∠2=∠D
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.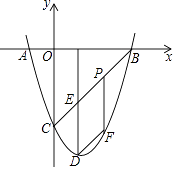
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( ) 
A.①
B.②
C.①②
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=5:2,则∠AOF等于( )

A. 140° B. 130° C. 120° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.
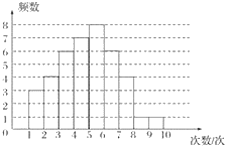
(1)求共抽取了多少名学生进行引体向上测试?
(2)试估计该校九年级学生引体向上次数不低于5次的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com