
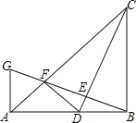
【题目】如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①![]() ;②若点D是AB的中点,则AF=
;②若点D是AB的中点,则AF=![]() AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若
AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若![]() ,则S△ABC=9S△BDF,其中正确的结论序号是______.
,则S△ABC=9S△BDF,其中正确的结论序号是______.
【答案】①②③
【解析】
由△AFG∽△CFB,可确定结论①正确;由△ABG≌△BCD可得AG=![]() AB=
AB=![]() BC,进而由△AFG∽△CFB确定点F为AC的三等分点,可确定结论②正确;当B、C、F、D四点在同一个圆上时,由圆内接四边形的性质得到∠CFD=∠ABC=90°,得到CD为圆的直径,因为BG⊥CD,根据垂径定理得到DF=DB,故③正确;因为D为AB的三等分点,△AFG∽△CFB,所以
BC,进而由△AFG∽△CFB确定点F为AC的三等分点,可确定结论②正确;当B、C、F、D四点在同一个圆上时,由圆内接四边形的性质得到∠CFD=∠ABC=90°,得到CD为圆的直径,因为BG⊥CD,根据垂径定理得到DF=DB,故③正确;因为D为AB的三等分点,△AFG∽△CFB,所以![]() 所以S△ABF=
所以S△ABF=![]() S△ABC,又S△BDF=
S△ABC,又S△BDF=![]() S△ABF,所以S△ABC=12S△BDF,由此确定结论④错误.
S△ABF,所以S△ABC=12S△BDF,由此确定结论④错误.
解:依题意可得BC∥AG,
∴△AFG∽△CFB,
∴![]() ,
,
又AB=BC,
∴![]() .故结论①正确;
.故结论①正确;
如图,
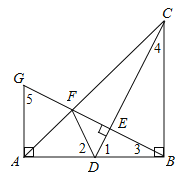
∵∠1+∠3=90°,∠1+∠4=90°,
∴∠3=∠4.
在△ABG与△BCD中,
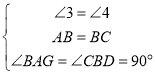 ,
,
∴△ABG≌△BCD(ASA),
∴AG=BD,
又∵BD=AD,
∴AG=AD;
∵△ABC为等腰直角三角形,
∴AC=![]() AB;
AB;
∴AG=AD=![]() AB=
AB=![]() BC;
BC;
∵△AFG∽△BFC,
∴![]() ,
,
∴FC=2AF,
∴AF=![]() AC=
AC=![]() AB.故结论②正确;
AB.故结论②正确;
当B、C、F、D四点在同一个圆上时,
由圆内接四边形的性质可得∠CFD=∠ABC=90°
∴CD是B、C、F、D四点所在圆的直径,
∵BG⊥CD,
∴![]() ,
,
∴DF=DB,故③正确;
∵![]() ,AG=BD,
,AG=BD,![]() ,
,
∴![]() ,
,
∴S△BDF=![]() S△ABF,
S△ABF,![]() ,
,
∴AF=![]() AC,
AC,
∴S△ABF=![]() S△ABC;
S△ABC;
∴S△BDF=![]() S△ABC,即S△ABC=12S△BDF.故结论④错误.
S△ABC,即S△ABC=12S△BDF.故结论④错误.
∴正确的结论有①②③;
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
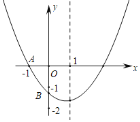
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和C(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2<8a;④![]() ;⑤b<c.其中含所有正确结论的选项是_____.
;⑤b<c.其中含所有正确结论的选项是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
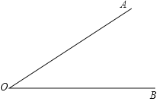
【题目】下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①在射线![]() 上任取一点
上任取一点![]() ;
;
②作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
③连接![]() ;
;
所以![]() 即为所求作的角.
即为所求作的角.
根据小华设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
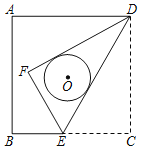
【题目】如图,已知边长为2的正方形ABCD,边BC上有一点E,将△DCE沿DE折叠至△DFE,若DF,DE恰好与以正方形ABCD的中心为圆心的⊙O相切,则⊙O的半径为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
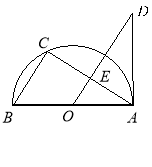
【题目】如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.
【1】求证:AD是半圆O的切线;
【2】若BC=2,CE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:![]() ,
,![]() ,
,![]() ,因此4,12,20都是“神秘数”
,因此4,12,20都是“神秘数”
(1)请说明28是否为“神秘数”;
(2)下面是两个同学演算后的发现,请选择一个“发现”,判断真假,并说明理由.
①小能发现:两个连续偶数![]() 和
和![]() (其中
(其中![]() 取非负整数)构造的“神秘数”也是4的倍数.
取非负整数)构造的“神秘数”也是4的倍数.
②小仁发现:2016是“神秘数”.
提示:(2)中两个发现,只需解答其中一个,若两个都做,按“小能发现”的解答计分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数![]() (x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数
(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数![]() (x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是______.
(x>0)的图象过点B,C,若△OAB的面积为6,则△ABC的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.元曲;D.论语.比赛形式分“单人组”和“双人组”.
(1)小明参加“单人组”,他从中随机抽取一个比赛项目,则抽到“唐诗”的是 事件,其概率是 ;
(2)若小亮和小丽组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小亮和小丽都没有抽到“元曲”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com