
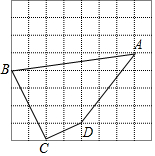
 如图,每个小正方形的边长为1,A、B、C、D均在小正方形的顶点上.
如图,每个小正方形的边长为1,A、B、C、D均在小正方形的顶点上.科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线互相垂直平分的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚普通正六面体骰子所得点数不超过6 | |
| B. | 买一张体育彩票中一等奖 | |
| C. | 从实数-$\frac{2}{7},\sqrt{3},\root{3}{-8},\frac{1}{3}$π,0.1010010001中随机抽取一个数恰好是有理数 | |
| D. | 口袋中装有10 个红球,从中摸出一个是白球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com