练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．已知正比例函数的图象经过点（2，-$\sqrt{3}$），求这个正比例函数的解析式．

    分析 设这个正比例函数的解析式是y=kx，再将（2，-$\sqrt{3}$）代入求得k即可．

    解答 解：设正比例函数的解析式为y=kx，图象经过点（2，-$\sqrt{3}$），得
    $-\sqrt{3}$=2k，
    解得k=-$\frac{\sqrt{3}}{2}$．
    ∴这个正比例函数的解析式为：y=-$\frac{\sqrt{3}}{2}$x．

    点评 本题考查了待定系数法求正比例函数解析式，把点的坐标代入函数解析式得出k值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．李明靠勤工俭学的收入支付生活费，下面是李明一周的收支情况表（收入为正，支出为负，单位为元）
    周一周二周三周四周五周六周日
    +15+100+20+15+10+17
    -8-12-10-7-9-8-10
    （1）在一周内李明有多少结余？
    （2）照这样，一个月（按30天计算）李明能有多少结余？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．（1）如图1，直线AB：y=-2x+8分别交x轴、y轴于点A、B，与直线OC：y=$\frac{6}{5}$x交于点C．
    求①点C的坐标；
    ②△OAC的面积．
    （2）如图2，已知直线OC：y=$\frac{6}{5}$x，作∠AOC的平分线ON，△OAC的面积为5，且OA=4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ+PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．在一条笔直的公路的同侧依次排列着A，C，B三个村庄，某天甲、乙两车分别从A，B两地出发，沿这条公路匀速行驶至C地停止，从甲车出发至甲车到达C地的过程，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．
    求：（1）甲的速度是60km/h，乙的速度是80km/h；
    （2）分别求出甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系式，并写出取值范围；
    （3）若甲、乙两车到C地后继续沿该公路原速度行驶，求甲车出发多少小时，两车相距350km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

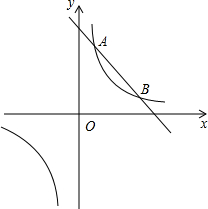    1．如图，反比例函数y1=$\frac{k}{x}$，（k＞0）与一次函数y2=-x+5交于A（2，n）、B两点（A点在B点左边）
    （1）求反比例函数y1的解析式和B的坐标；
    （2）平移y2的图象，使得平移后的直线交反比例函数y1的图象于E、F两点（E点在F点左边），若EF=2AB，直接写出点E的横坐标（-$\sqrt{7}$-1，-$\sqrt{7}$+1）或（$\sqrt{7}$-1，$\sqrt{7}$+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，O为坐标原点，抛物线F：y=ax2+2ax+c经过A（-4，0），B（0，4）两点，与x轴交于另一点C，直线y=x+5与x轴交于点D，与y轴交于点E．
    （1）求抛物线的解析式及顶点坐标；
    （2）求点B关于直线y=x+5的对称点B′，并判断点B′是否在抛物线的对称轴上；
    （3）画出函数y=|ax2+2ax+c|的图象F′，并写出过点B且与图象F′恰有三个公共点的直线表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．将函数y=2x+b（b为常数）的图象位于x轴上方的部分沿x轴翻折至其下方后，所得的折线是函数y=-|2x+b|（b为常数）的图象．若该图象在直线y=-4上方的点的横坐标x满足0＜x＜5．求b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，某小区楼房附近有一个斜坡，小张发现楼房在水平地面与斜坡处形成的投影中，在斜坡上的影子长CD=6m，坡角到楼房的距离CB=8m．在D点处观察点A的仰角为60°，已知坡角为30°，你能求出楼房AB的高度吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

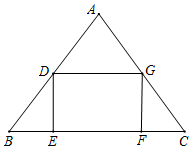    16．如图，在△ABC中，AB=AC=10，BC=12，矩形DEFG的顶点位于△ABC的边上，设EF=x，S四边形DEFG=y．
    （1）填空：自变量x的取值范围是0＜x＜12；
    （2）求出y与x的函数表达式；
    （3）请描述y随x的变化而变化的情况．

    查看答案和解析>>

    同步练习册答案