
【题目】如图:直线AB经过点A(0,3)点B( ![]() ,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C.
,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C. 
(1)求直线AB的解析式;
(2)求点M的坐标;
(3)点P是劣弧AC上一个动点,当P点运动时,问:线段PA,PB,PC有什么数量关系?并给出证明.
【答案】
(1)解:设直线AB的解析式为y=kx+b,
把点A(0,3)和点B( ![]() ,0)代入y+kx+b得到
,0)代入y+kx+b得到 ![]() ,
,
解得 ![]() ,
,
∴直线AB的解析式为y=﹣ ![]() x+3
x+3
(2)解:如图1中,连接BM.设AM=BM=r.
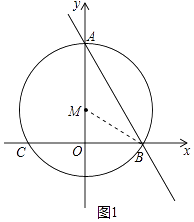
在Rt△BMO中,
∵OM2+OB2=BM2,OM=3﹣r,OB= ![]() ,
,
∴(3﹣r)2+( ![]() )2=r2,
)2=r2,
∴r=2,
∴OM=3﹣2=1,
∴点M坐标为(0,1)
(3)解:结论:PB=PA+PC,理由如下:
如图2中,连接AC、在PB上截取PN=PC,连接CN.
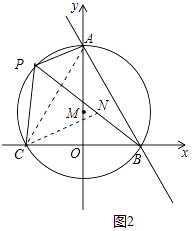
∵OM⊥BC,
∴OC=OB,
∴AC=AB,
∵tan∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AC=CB,∠ACB=∠CAB=60°,
∴∠CPB=∠CAB=60°,∵PC=PN,
∴△PCN是等边三角形,
∴CP=CN,∠PCN=60°,
∴∠PCN=∠ACB=60°,
∴∠PCA=∠NCB,∵PC=CN,CA=CB,
∴△PCA≌△NCB,
∴PA=BN,
∵PB=PN+BN,PN=PC,BN=PA,
∴PB=PA+PC.
【解析】(1)设直线AB的解析式为y=kx+b,把点A(0,3)和点B( ![]() ,0)代入y+kx+b得到
,0)代入y+kx+b得到 ![]() 解方程组即可.(2)如图1中,连接BM.设AM=BM=r.在Rt△BMO中,由OM2+OB2=BM2 , OM=3﹣r,OB=
解方程组即可.(2)如图1中,连接BM.设AM=BM=r.在Rt△BMO中,由OM2+OB2=BM2 , OM=3﹣r,OB= ![]() ,可得(3﹣r)2+(
,可得(3﹣r)2+( ![]() )2=r2 , 解方程即可.(3)结论:PB=PA+PC,如图2中,连接AC、在PB上截取PN=PC,连接CN.首先证明△ACB,△PCN都是等边三角形,再证明△PCA≌△NCB,推出PA=BN,由此即可解决问题.
)2=r2 , 解方程即可.(3)结论:PB=PA+PC,如图2中,连接AC、在PB上截取PN=PC,连接CN.首先证明△ACB,△PCN都是等边三角形,再证明△PCA≌△NCB,推出PA=BN,由此即可解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知a,b,c满足(a-![]() )2+
)2+![]() +
+![]() =0.
=0.
(1)求a,b,c的值.
(2)以a,b,c为边能否构成三角形?若能构成,求出该三角形的周长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意设未知数,并列出方程(不必求解).
(1)有两个工程队,甲队人数30名,乙队人数10名,问怎样调整两队的人数,才能使甲队的人数是乙队人数的7倍.
(2)有一个班的同学准备去划船,租了若干条船,他们计算了一下,如果比原计划多租1条船,那么正好每条船坐6人;如果比原计划少租1条船,那么正好每条船坐9人.问这个班共有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师要为他家的长方形餐厅(如图1)选择一张餐桌,并且想按如下要求摆放:餐桌一侧靠墙,靠墙对面的桌边留出宽度不小于80 cm的通道,另两边各留出宽度不小于60 cm的通道.那么在图2的四张餐桌中,其规格符合要求的餐桌编号是________.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(+4)×(-5); (2)(-0.125)×(-8);
(3)(-2![]() )×(-
)×(-![]() ); (4)0×(-13.52);
); (4)0×(-13.52);
(5)(-3.25)×(+![]() ); (6)(-1)×a.
); (6)(-1)×a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点E,则△DEF的面积为______.
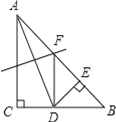
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是 ![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°.
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°. 
(1)求∠ABC的度数;
(2)若CM=4 ![]() ,求
,求 ![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com