
【题目】阅读可以增进人们的知识也能陶冶人们的情操.我们要多阅读,多阅读有营养的书.因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
请结合以上信息解答下列问题
(1)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在![]() 以下(不含
以下(不含![]() )的学生所占百分比.
)的学生所占百分比.

【答案】(1)20;40;200;(2)作图见解析;(3)24%.
【解析】分析:(1)根据D类的人数是140,所占的比例是28%,即可求得总人数,然后根据百分比的意义求得c的值,同理求得A、B两类的总人数,则a的值即可求得,进而求得b的值;(2)根据(1)的结果即可作出;(3)根据百分比的定义即可求解.
本题解析:(1)总人数是:140÷28%=500,
则c=500×8%=40,
A. B两类的人数的和是:500×(140%28%8%)=120,
则a=120100=20,
b=50012014040=200;
(2)补全图如图所示
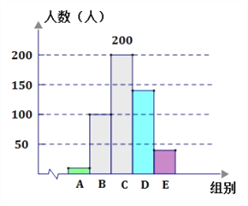
(3)由(1)可知 ![]()
答:估计全校课外阅读时间在20h以下的学生所占百分比为24%.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为![]() 个单位长度的半圆
个单位长度的半圆![]() ,
, ![]() ,
, ![]() …….组成一条平滑的曲线,点
…….组成一条平滑的曲线,点![]() 从原点
从原点![]() 出发,沿这条曲线向右运动,速度为每秒
出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第
个单位长度,则第![]() 时,点
时,点![]() 的坐标是( )
的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
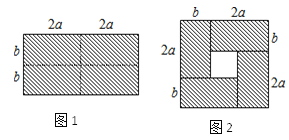
【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2中的空白部分的边长是多少?(用含a,b的式子表示)
(2)观察图2,请根据图形的面积关系用等式表示出(2a﹣b)2,ab和(2a+b)2之间的数量关系;
(3)若2a+b=7,ab=3,求图2中的空白正方形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
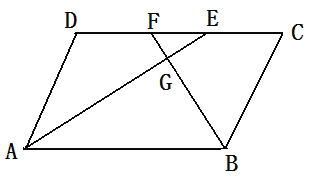
【题目】平行四边形ABCD中, AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.
(1)求证AE⊥BF
(2)判断DE和CF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
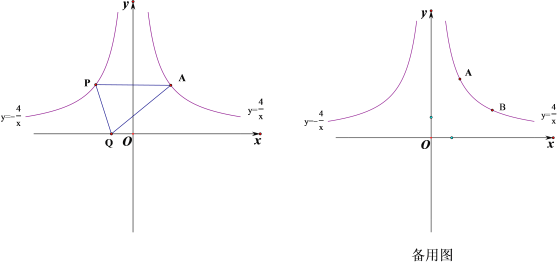
【题目】平面直角坐标系xOy中,已知函数y1=![]() (x>0)与y2=﹣
(x>0)与y2=﹣![]() (x<0)的图象如图所示,点A、B是函数y1=
(x<0)的图象如图所示,点A、B是函数y1=![]() (x>0)图象上的两点,点P是y2=﹣
(x>0)图象上的两点,点P是y2=﹣![]() (x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(1)求△APQ的面积;
(2)若△APQ是等腰直角三角形,求点Q的坐标;
(3)若△OAB是以AB为底的等腰三角形,求mn的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com