练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点P1（1，1），点P2（2，2）是一次函数＝－4 + 3 图象上的两个点，且1＜2，则1与2的大小关系是（     ）

    （A）1＞2       （B）1＞2＞0      （C）1＜2     （D）1＝2

     

    【答案】

    A

    【解析】

    试题分析：根据题意，k=-4＜0，y随x的增大而减小，因为x1＜x2，所以y1＞y2．

    考点：一次函数图象上点的坐标特征

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

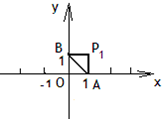    18、如果将点P绕定点M旋转180°后与点Q重合，那么点P与点Q关于点M对称，定点M叫对称中心，此时，点M是线段PQ的中点．如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0），点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称，点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，…，且这些对称中心依次循环，已知P1的坐标是（1，1），点P100的坐标为
    （1，-3）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于点M对称，定点M叫做对称中心。此时，M是线段PQ的中点。

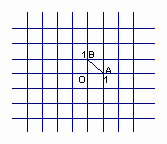
    　　 如图，在直角坐标系中，⊿ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0）。点列P1、P2、P3、…中的相邻两点都关于⊿ABO的一个顶点对称：点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，…。对称中心分别是A、B，O，A，B，O，…，且这些对称中心依次循环。已知点P1的坐标是（1，1），试求出点P2、P7、P100的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

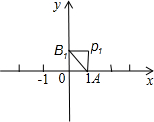    如果将点P绕定点M旋转180°后与点Q重合，那么点P与点Q关于点M对称，定点M叫对称中心，此时，点M是线段PQ的中点．如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0），点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称，点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，…，且这些对称中心依次循环，已知P1的坐标是（1，1），点P100的坐标为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，是12×12的正方形（每个小正方形边长均为1个单位）的网格．
    （1）在图①中建立适当的直角坐标系使点P1，P3的坐标分别为（-1，2）、（1，-1）．将图A通过平移或旋转这两种变换得到图C可用以下三种办法：
    方法1：将图形A向______（填“上”或“下”）平移______个单位，得到图形B，再将图形B向右平移______个单位后，再绕点P2按顺时针方向旋转______得到图形C；
    方法2：先将图形A平移到图形B，再将图形B绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是______；
    方法3：直接将图形A绕某点R顺时针旋转______°得到图形C，则点R的坐标是______；
    （2）在图②中画一个格点四边形EFGH，使它为轴对称图形且面积等于图A面积的3倍（除矩形外）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“非常距离”，给出如下定义：

    若|x1﹣x2|≥|y1﹣y2|，则点P1与点P2的“非常距离”为|x1﹣x2|；

    若|x1﹣x2|＜|y1﹣y2|，则点P1与点P2的“非常距离”为|y1﹣y2|．

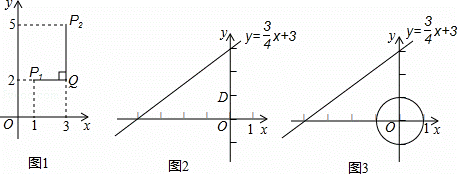
    例如：点P1（1，2），点P2（3，5），因为|1﹣3|＜|2﹣5|，所以点P1与点P2的“非常距离”为|2﹣5|=3，也就是图1中线段P1Q与线段P2Q长度的较大值（点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点）．

    （1）已知点A（﹣，0），B为y轴上的一个动点，

    ①若点A与点B的“非常距离”为2，写出一个满足条件的点B的坐标；

    ②直接写出点A与点B的“非常距离”的最小值；

    （2）已知C是直线y=x+3上的一个动点，

    ①如图2，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标；

    ②如图3，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标．

    　

    查看答案和解析>>

    同步练习册答案