
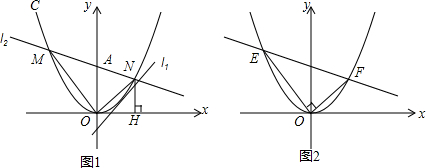
分析 (1)首先将l1和抛物线C的解析式联立得:ax2-x+1=0,由直线l1:y=x-1与抛物线C有且只有1个交点,可得△=0,继而求得a的值,即求得抛物线C的解析式;
(2)首先设l2解析式为y=kx+b,然后与抛物线C解析式联立,再设点M(x1,kx1+4),N(x2,kx2+4),分别表示出OM,ON的斜率,然后求得k1k2=-1,即可证得OM⊥ON,则可求得l2的解析式;
(3)与(2)类似,可以由k1k2=-1,求得G点坐标.
解答 解:(1)将l1和抛物线C的解析式联立得:ax2-x+1=0,
∵y=x-1与抛物线C有且只有1个交点,
∴△=1-4a=0,
解得a=$\frac{1}{4}$,
∴C的解析式为y=$\frac{1}{4}$x2;
(2)假设存在l2,设l2解析式为y=kx+b,
与抛物线C解析式联立得:$\frac{1}{4}$x2-kx-4=0,
设点M(x1,kx1+4),N(x2,kx2+4),
则直线OM、ON的斜率分别为k1=$\frac{k{x}_{1}+4}{{x}_{1}}$,k2=$\frac{k{x}_{2}+4}{{x}_{2}}$,
∴k1k2=k2+$\frac{4k({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$+$\frac{16}{{x}_{1}{x}_{2}}$,
∵x1+x2=4k,x1•x2=-16,
∴k1k2=k2+$\frac{16{k}^{2}}{-16}$+$\frac{16}{-16}$=-1,
∴OM⊥ON恒成立,∠MON=∠NHO=90°,
要想使△MON∽△NHO成立,只需再令∠MNO=∠NOH即可,
即MN⊥y轴,
∴存在l2符合题意,l2解析式为y=4;
(3)存在定点G,
假设存在l,设l解析式为y=kx+b,
与抛物线C解析式联立得:ax2-kx-b=0,
设点M(x1,kx1+b),N(x2,kx2+b),
则直线OM、ON的斜率分别为k1=$\frac{k{x}_{1}+b}{{x}_{1}}$,k2=$\frac{k{x}_{2}+b}{{x}_{2}}$,
∴k1k2=k2+$\frac{bk({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$+$\frac{{b}^{2}}{{x}_{1}{x}_{2}}$,
∵x1+x2=$\frac{k}{a}$,x1•x2=-$\frac{b}{a}$,OE⊥OF,
∴k1k2=k2+$\frac{bk•\frac{k}{a}}{-\frac{b}{a}}$+$\frac{{b}^{2}}{-\frac{b}{a}}$=-ab=-1,
∴b=$\frac{1}{a}$,
∴点G坐标为(0,$\frac{1}{a}$).
点评 本题考查了二次函数的综合题.考查了一次函数与二次函数的交点问题,属于新定义题目.注意理解斜率的定义是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 能够完全重合的图形称为全等图形 | |
| B. | 全等图形的形状和大小都相同 | |
| C. | 所有正方形都是全等图形 | |
| D. | 两边及两边的夹角对应相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
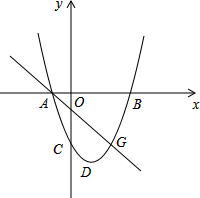 如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
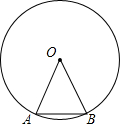 如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上,将正三角形OAB沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点B运动的路径长为( )
如图边长为2的正三角形OAB的顶点A、B在一个半径为2的圆上,将正三角形OAB沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点B运动的路径长为( )| A. | 4π | B. | 2π | C. | $\frac{10}{3}$π | D. | $\frac{8}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
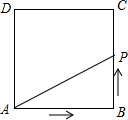 如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→→D→A,设P点经过的路程为x,以点A、P、B为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→→D→A,设P点经过的路程为x,以点A、P、B为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )| A. | 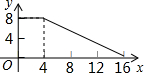 | B. | 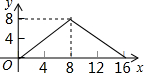 | C. | 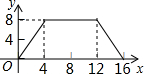 | D. | 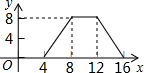 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com