
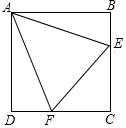
 已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$. 分析 如图将△ABE绕点A顺时针旋转90°得到△ADM,作FH⊥AE于H.首先证明△FAE≌△FAM,推出EF=FM,S△FAE=S△FAM,由FH⊥AE,∠FAH=45°,推出FH=AF•sin45°=$\frac{\sqrt{2}}{2}$AF,由S△AEF=$\frac{1}{2}$•AE•FH=$\frac{1}{2}$•AE•$\frac{\sqrt{2}}{2}$AF=$\frac{\sqrt{2}}{4}$•AE•AF=$\frac{20}{3}$,由$\frac{1}{2}$•EF•AD=$\frac{20}{3}$,即可推出EF=$\frac{10}{3}$.
解答 解:如图将△ABE绕点A顺时针旋转90°得到△ADM,作FH⊥AE于H.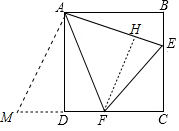
∵四边形ABCD是正方形,
∴∠DAB=90°,∵∠EAF=45°,
∴∠BAE+∠DAF=∠DAF+∠MAD=45°,
∴∠FAE=∠FAM,
在△FAE和△FAM中,
$\left\{\begin{array}{l}{FA=FA}\\{∠FAE=∠FAM}\\{AE=AM}\end{array}\right.$,
∴△FAE≌△FAM,
∴EF=FM,S△FAE=S△FAM,
∵FH⊥AE,∠FAH=45°,
∴FH=AF•sin45°=$\frac{\sqrt{2}}{2}$AF,
∵S△AEF=$\frac{1}{2}$•AE•FH=$\frac{1}{2}$•AE•$\frac{\sqrt{2}}{2}$AF=$\frac{\sqrt{2}}{4}$•AE•AF=$\frac{20}{3}$,
∴$\frac{1}{2}$•EF•AD=$\frac{20}{3}$,
∴EF=$\frac{10}{3}$
故答案为$\frac{10}{3}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、三角形的面积、等腰直角三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
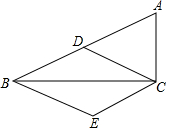 如图,Rt△ABC中点D是AB中点,过点B,点C分别作BE∥CD,CE∥BD.
如图,Rt△ABC中点D是AB中点,过点B,点C分别作BE∥CD,CE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
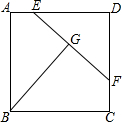 如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.
如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
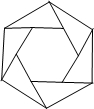 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )| A. | ($\sqrt{2}$)2016倍 | B. | ($\sqrt{3}$)2017倍 | C. | ($\sqrt{3}$)2018倍 | D. | ($\sqrt{2}$)2019倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
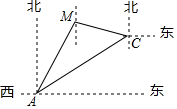 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
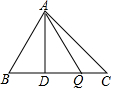 如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )| A. | S=80-5x | B. | S=5x | C. | S=10x | D. | S=5x+80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a6÷a3=a2 | B. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | C. | (-1)-1=1 | D. | (a3)2=a5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com