
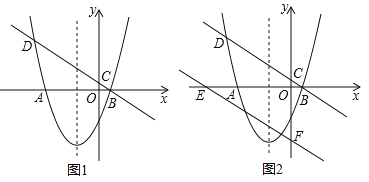
����Ŀ����ͼ1��������y=ax2+2x+c��x�ύ��A����4��0����B��1��0�����㣬����B��ֱ��y=kx+![]() �ֱ���y�ἰ�����߽��ڵ�C��D��
�ֱ���y�ἰ�����߽��ڵ�C��D��
��1����ֱ�ߺ������ߵı���ʽ��
��2������P�ӵ�O��������x��ĸ���������ÿ��1����λ���ȵ��ٶ����������˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����PDCΪֱ�������Σ���ֱ��д����������������t��ֵ��
��3����ͼ2����ֱ��BD��y������ƽ��4����λ����x�ᣬy��ֱ���E��F���㣬�������ߵĶԳ������Ƿ���ڵ�M����ֱ��EF���Ƿ���ڵ�N��ʹDM+MN��ֵ��С�������ڣ��������Сֵ����M��N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�������߽���ʽΪ��y=![]() ��BD����ʽΪy=��
��BD����ʽΪy=��![]() ����2��t��ֵΪ
����2��t��ֵΪ![]() ��
��![]() ��
��![]() ����3��N����������2����2����M����������
����3��N����������2����2����M����������![]() ����
����![]() ����
����![]() .
.
����������1�����ô���ϵ�������ɵã�
��2������õ�D�����꣬����D�ֱ���DE��x�ᡢDF��y�ᣬ��P1D��P1C��P2D��DC��P3C��DC����������������������ε�������һ���ɵã�
��3��ͨ�����ԳƵ㣬������ת�����������룬Ӧ������֮���߶���̣�
��1����A����4��0����B��1��0������y=ax2+2x+c��
��![]() ��
��
��ã�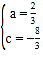 ��
��
�������߽���ʽΪ��y=![]() ��
��
�߹���B��ֱ��y=kx+![]() ��
��
����루1��0�����ã�k=��![]() ��
��
��BD����ʽΪy=��![]() ��
��
��2����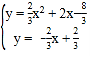 �ý�������ΪD����5��4����
�ý�������ΪD����5��4����
��ͼ1����D��DE��x���ڵ�E����DF��y���ڵ�F��
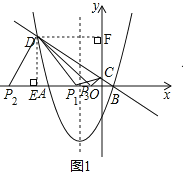
��P1D��P1Cʱ����P1DCΪֱ�������Σ�
����DEP1�ס�P1OC��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
���t=![]() ��
��
��P2D��DC�ڵ�Dʱ����P2DCΪֱ��������
����P2DB�ס�DEB��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��ã�t=![]() ��
��
��P3C��DCʱ����DFC�ס�COP3��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�t=![]() ��
��
��t��ֵΪ![]() ��
��![]() ��
��![]() ��
��
��3������ֱ֪��EF����ʽΪ��y=��![]() x��
x��![]() ��
��
����������ȡ��D�ĶԳƵ�D��������D����D��N��EF�ڵ�N���������߶Գ����ڵ�M
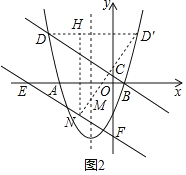
����N��NH��DD���ڵ�H����ʱ��DM+MN=D��N��С��
����EOF�ס�NHD��
���N������a����![]() ����
����
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�a=��2��
��N����������2����2����
���ֱ��ND���Ľ���ʽΪy=![]() x+1��
x+1��
��x=��![]() ʱ��y=��
ʱ��y=��![]() ��
��
��M����������![]() ����
����![]() ����
����
��ʱ��DM+MN��ֵ��СΪ![]() =
=![]() =2
=2![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���A����B ����C�� ��D �Ľ�ƽ����ǡ�ཻ��һ��P��������APD����APB����BPC����DPC������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �����й�ϵʽ��ȷ���ǣ� ��
�����й�ϵʽ��ȷ���ǣ� ��
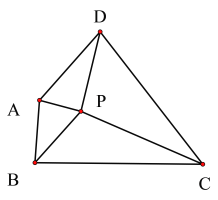
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ַ�����¥�̵ijɽ���Ѹ���½�����ͳ�ƣ���������ǰij���ȶ��ַ�����¥�̳ɽ���Ϊ9500�ף�����ͬһ���ȶ��ַ�����¥�̵ijɽ�����4425�ף����ж��ַ��ɽ�������ǰ����55������¥�̳ɽ�������ǰ����52����
��1����������ַ�����¥�̸��ɽ������ף�
��2���ڳɽ����µ���ͬʱ������Ҳ�����ˮ.ij¥����ǰ����Ϊ12000Ԫ/m2,���������ʽ��۽��е����������µ������Ϊ7680Ԫ/m2����ƽ��ÿ���µ��İٷ��ʣ�������̬���÷��ۻع������λ��������λΪ�����ǿ�֧�������3��6�������轭��ƽ��ÿ����ͥ������֮�ң������֧������Ϊ9��Ԫ��ÿ����ͥ��ƽ��ס�����Ϊ80 m2�����µ���ķ��ۻص�������λ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AD��AB��AM��BN��CP��DQΪ�ĸ��ڽǵĽ�ƽ���ߣ�P��ΪAD�������㣬����AM��DQ�ཻ��E��BN��CP�ཻ��F��AM��BN�ཻ��G��CP��DQ�ཻ��H��
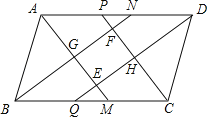
��1����֤���ı���EHFG�Ǿ��Σ�
��2��ABCD������ ʱ���ı���EHFGΪ�����Σ�ABCD������ ʱ��F������AD���ϣ������P����N�غϣ�
��3��̽������EHFG�ĶԽ��߳�����ABCD�ı߳�֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ͼ������֪������y=��![]() x2+bx+c������A����1��0���͵�B��0��
x2+bx+c������A����1��0���͵�B��0��![]() ��������ΪC����D����Գ�������λ�ڵ�C�·������߶�DC�Ƶ�D��˳ʱ�뷽����ת90������C�����������ϵĵ�P����
��������ΪC����D����Գ�������λ�ڵ�C�·������߶�DC�Ƶ�D��˳ʱ�뷽����ת90������C�����������ϵĵ�P����
��1�������������ߵı���ʽ��
��2�����߶�CD�ij���
��3����������ƽ�ƣ�ʹ�䶥��C�Ƶ�ԭ��O��λ�ã���ʱ��P���ڵ�E��λ�ã������M��y���ϣ�����O��D��E��MΪ������ı������Ϊ8�����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ի�����ٿ��ڼ䣬�����Ĵ�ѧ��־Ը�߲��������.ij��ѧ�ƻ���֯��Уȫ��־Ը��ͳһ�˳�ȥ�᳡������������36������Դ�ͳ�������������2��û����λ����ֻ����22������Դ�ͳ������ó�����������4�������ճ�2����λ.
(1)�ƻ�����36������Դ�ͳ����������ô�ѧ���ж�����־Ը�ߣ�
(2)��ͬʱ����36����22�����ֳ��ͣ��ȱ�֤ÿ���������ֱ�֤ÿ���������������ֳ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P��a��b���͵�Q��a��b'�����������¶��壺
��b'=![]() ����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
��1���ٵ㣨��![]() ��1�����ޱ����������� ����
��1�����ޱ����������� ����
���ڵ�A����1��2����B����2����1������һ�����Ǻ���y=![]() ͼ����ijһ��������㣬��������� ����
ͼ����ijһ��������㣬��������� ����
��2������P�ں���y=��x+3��ͼ���ϣ�����2��x��6ʱ�������ޱ��Q��������b'��ȡֵ��Χ��
��3������P�ڹ���x�Ķ��κ���y=x2��2tx+t2+t��ͼ���ϣ����ޱ��Q��������b'��ȡֵ��Χ��b'��m��b'��n������m��n����s=m��n����s����t�ĺ�������ʽ��s��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1,������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() �͵�
�͵�![]() ,��
,��![]() �ύ�ڵ�
�ύ�ڵ�![]() ,������
,������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ���ڵ�
���ڵ�![]() ����������
����������![]() ƽ�ƺ�õ�����Ϊ
ƽ�ƺ�õ�����Ϊ![]() �ҶԳ���Ϊֱ
�ҶԳ���Ϊֱ![]() ��������
��������![]() ��
��
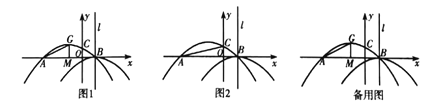
(1)��������![]() �Ľ���ʽ��
�Ľ���ʽ��
(2)��ͼ2,��ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ,ʹ
,ʹ![]() �ǵ���������?������,��������е�
�ǵ���������?������,��������е�![]() ������:��������,��˵��������
������:��������,��˵��������
(3)��![]() ������
Ϊ������![]() ��һ����,����
��һ����,����![]() ��
��![]() ���ƽ���߽�������
���ƽ���߽�������![]() �ڵ�
�ڵ�![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() �������������
Ϊ�������������![]() ȫ��,��ֱ��
ȫ��,��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
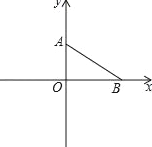
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬A��B���������ֱ�ΪA(0��m)��B(n��0)����|m��n��3|+![]() ��0����P��A��������ÿ��1����λ���ٶ�������AO�����˶������P���˶�ʱ��Ϊt�룮
��0����P��A��������ÿ��1����λ���ٶ�������AO�����˶������P���˶�ʱ��Ϊt�룮
(1)��OA��OB�ij���
(2)����PB�����POB�����ΪS����t��ʽ�ӱ�ʾS��
(3)����P��ֱ��AB�Ĵ��ߣ�����ΪD��ֱ��PD��x�ύ�ڵ�E���ڵ�P�˶��Ĺ����У��Ƿ���������ĵ�P��ʹ��EOP�ա�AOB�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com