
【题目】如图,在△ABC中,∠ACB=90°,AC=2![]() ,BC=4
,BC=4![]() ,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作EDFP,设点P的运动时间为t(秒).
,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作EDFP,设点P的运动时间为t(秒).

(1)求AB长.
(2)当∠DPF=∠PFD时,求t的值.
(3)当点P在线段CD上时,设EDFP与△ABC重叠部分图形的面积为y(平方单位),求y与t之间的函数关系式.
(4)连结AF,当△AFD的面积与△PDE的面积相等时,直接写出t的值.
【答案】(1)10;(2)![]() .(3) y=
.(3) y=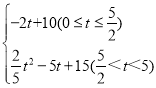 .(4) 0或
.(4) 0或![]() .
.
【解析】
试题分析:(1)在RT△ABC中利用勾股定理即可解决问题.
(2)如图1中,当∠DPF=∠PFD时,可以证明PE∥AB,PC=PD,由此即可解决问题.
(3)分两种情形①当0≤t≤![]() 时,如图2中,作PM⊥DE存在为M,此时重叠部分面积就是平行四边形PEDF的面积,②当
时,如图2中,作PM⊥DE存在为M,此时重叠部分面积就是平行四边形PEDF的面积,②当![]() <t<5时,如图3中,此时y=S△PHD+S△PDE.
<t<5时,如图3中,此时y=S△PHD+S△PDE.
(4)两种情形①t=O时,△ADF与△PDE面积相等.②如图4中,当A、P、E共线时△ADF与△PDE面积相等,由DE∥AC得![]() ,求出PC即可.
,求出PC即可.
试题解析:(1)在△ABC中,∵∠ACB=90°,AC=2![]() ,BC=4
,BC=4![]() ,
,
∴AB=![]() .
.
(2)如图1中,
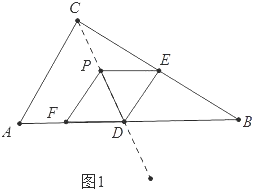
∵四边形PEDF是平行四边形,
∴PF∥DE,PE∥DF,
∴∠DPF=∠PDE,
∵∠ACB=90°,AD=DB,
∴CD=DB=DA=5,∵CE=EB,
∴DE⊥BC,∠CDE=∠EDB
∵∠DPF=∠PFD,
∴∠PED=∠BDE,
∴PE∥DB,∵CE=EB,
∴PC=PD=![]() ,
,
∴t=![]() .
.
(3)①当0≤t≤![]() 时,如图2中,
时,如图2中,
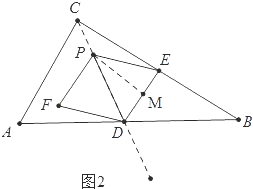
作PM⊥DE存在为M,
∵PM∥CE,
∴![]() ,
,
∴![]() ,
,
∴PM=![]() (5-t),
(5-t),
∴y=DEPM=![]()
![]() (5-t)=-2t+10.
(5-t)=-2t+10.
②当![]() <t<5时,如图3中,
<t<5时,如图3中,
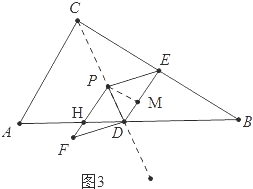
∵PH∥AC,
∴![]() ,
,
∴![]() ,
,
∴H=![]() (5-t),
(5-t),
∴y=S△PHD+S△PDE=![]() PHPM+
PHPM+![]() (-2t+10)=
(-2t+10)=![]() t2-5t+15,
t2-5t+15,
综上所述:y=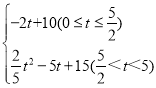 .
.
(4)①t=O时,△ADF与△PDE面积相等.
②如图4中,
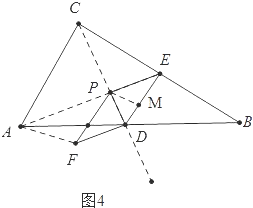
当A、P、E共线时,∵AE∥DF,
∴S△ADF=S△PDF=S△PED,
∵DE∥AC,
∴![]() ,
,
∴PC=![]() ,
,
∴t=![]() ,
,
∴t=0或![]() 时,△ADF与△PDE面积相等.
时,△ADF与△PDE面积相等.


科目:初中数学 来源: 题型:
【题目】用四舍五入法,按括号里的要求对下列各数取近似值:
(1)0.65148(精确到千分位); (2)1.5673(精确到0.01);
(3)450600(精确到千位)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为( )
A. 9 B. 10 C. 11 D. 以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆柱的体积计算公式是:圆柱体积=底面积×高.用计算器求高为0.82m,底面半径为0.47m的圆柱的体积(π取3.14,结果保留2个有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场6月份随即调查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.0,3.1,3.7,试估算该商场6月份总营业额大约是( )
A. 84万元 B. 96万元
C. 93万元 D. 111万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.
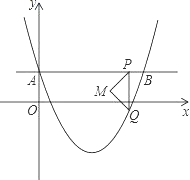
(1)求这条抛物线所对应的函数表达式.
(2)当线段PQ被x轴平分时,求m的值.
(3)当等腰直角三角形PQM夹在x轴与直线AB之间的图形为轴对称三角形时,求m的取值范围.
(4)直接写出当等腰直角三角形PQM的两条直角边与坐标轴有两个公共点时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
类别 | 成绩 | 频数 |
甲 | 60≤m<70 | 5 |
乙 | 70≤m<80 | a |
丙 | 80≤m<90 | 10 |
丁 | 90≤m≤100 | 5 |

根据图表信息,回答下列问题:
(1)该班共有学生________人;表中a=________;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+4x+1=0,配方后的方程是( )
A. (x+2)2=3 B. (x﹣2)2=3 C. (x﹣2)2=5 D. (x+2)2=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com