
��1����ͼ1,�ڵȱߡ�ABC��,��M�DZ�BC�ϵ�����һ�㣨�����˵�B��C��,����AM,��AMΪ�����ȱߡ�AMN,����CN����֤����ABC=��ACN��
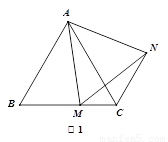
�����̽����
��2����ͼ2,�ڵȱߡ�ABC��,��M�DZ�BC�ӳ����ϵ�����һ�㣨�����˵�C��,������������,��1���н��ۡ�ABC=��ACN����������˵�����ɣ�

����չ���졿
��3����ͼ3,�ڵ�����ABC��,BA=BC,��M�DZ�BC�ϵ�����һ�㣨�����˵�B��C��,����AM,��AMΪ����������AMN,ʹ���ǡ�AMN=��ABC������CN����̽����ABC���ACN��������ϵ,��˵�����ɣ�
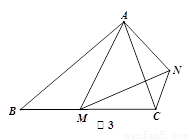
֤��������.
��������
�����������1����֤��BAM�ա�CAN������ȫ�����������ʵõ����ۣ�
��2����֤��BAM�ա�CAN������ȫ�����������ʵõ����ۣ�
��3����֤��ABC�ס�AMN,��֤��BAM�ס�CAN,���������������ʵõ����ۡ�
�����������1���ߡ�ABC����AMN�ǵȱ�������,
��AB=AC,AM=AN,��BAC=��MAN=60��,
���BAM=��CAN,
���BAM�ա�CAN��SAS��,
���ABC=��ACN��
��2�����ۡ�ABC=��ACN�Գ�����
�������£��ߡ�ABC����AMN�ǵȱ�������,
��AB=AC,AM=AN,
��BAC=��MAN=60��,
���BAM=��CAN,
���BAM�ա�CAN��SAS��,
���ABC=��ACN��
��3����ABC=��ACN��
�������£�
��BA=BC,MA=MN,���ǡ�ABC=��AMN,
��ǡ�BAC=��MAN,
���ABC�ס�AMN,
��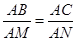 ,
,
�֡ߡ�BAM=��BAC����MAC,��CAN=��MAN����MAC,
���BAM=��CAN,
���BAM�ס�CAN,
���ABC=��ACN��
���㣺�����ε�ȫ��������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
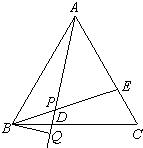 28����֪����ͼ���ڵȱ�������ABC�У�D��E�ֱ�ΪBC��AC�ϵĵ㣬��AE=CD������AD��BE���ڵ�P����BQ��AD������ΪQ����֤��BP=2PQ��
28����֪����ͼ���ڵȱ�������ABC�У�D��E�ֱ�ΪBC��AC�ϵĵ㣬��AE=CD������AD��BE���ڵ�P����BQ��AD������ΪQ����֤��BP=2PQ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
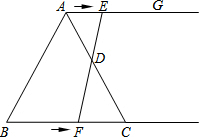 ��2013•���ϣ���ͼ���ڵȱ�������ABC�У�BC=6cm������AG��BC����E�ӵ�A����������AG��1cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt��s����
��2013•���ϣ���ͼ���ڵȱ�������ABC�У�BC=6cm������AG��BC����E�ӵ�A����������AG��1cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
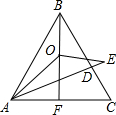 ��2012•��������ͼ���ڵȱ�������ABC�У�D��BC���ϵ�һ�㣬�ӳ�AD��E��ʹAE=AC����BAE��ƽ���߽���ABC�ĸ�BF�ڵ�O����tan��AEO=
��2012•��������ͼ���ڵȱ�������ABC�У�D��BC���ϵ�һ�㣬�ӳ�AD��E��ʹAE=AC����BAE��ƽ���߽���ABC�ĸ�BF�ڵ�O����tan��AEO=
| ||
| 3 |
| ||
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
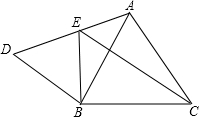 ��֪����ͼ���ڵȱߡ�ABC�͵ȱߡ�DBE�У���A��DE���ӳ����ϣ������ECB=38�㣬��ô��DAB=
��֪����ͼ���ڵȱߡ�ABC�͵ȱߡ�DBE�У���A��DE���ӳ����ϣ������ECB=38�㣬��ô��DAB=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
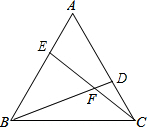 ��ͼ���ڵȱ�������ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬CD=AE������BD��CE���ڵ�F�����BFC=
��ͼ���ڵȱ�������ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬CD=AE������BD��CE���ڵ�F�����BFC=�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com